题目内容
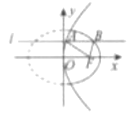
【题目】已知圆C：x2+y2+2x-4y+3=0．
（1）若圆C的切线在x轴、y轴上的截距相等，求切线的方程；
（2）从圆C外一点P（x1 ， y1）向圆引一条切线，切点为M，O为坐标原点，且有|PM|=|PO|，求使|PM|最小的点P的坐标．
【答案】
（1）解：由方程x2+y2+2x+4y+3=0知（x+1）2+（y-2）2=2，所以圆心为（-1，2），半径为 
．
当切线过原点时，设切线方程为y=kx，则 
= ，所以k=2± 
，即切线方程为y=（2± ）x．
当切线不过原点时，设切线方程为x+y=a，则 
= ，所以a=1或a=3，即切线方程为x+y+1=0或x+y3=0．
综上知，切线方程为y=（2± ）x或x+y+1=0或x+y-3=0；
（2）因为|PO|2+r2=|PC|2，所以x12+y12+2=（x1+1）2+（y1-2）2，即2x1-4y1+3=0．
要使|PM|最小，只要|PO|最小即可．
当直线PO垂直于直线2x-4y+3=0时，即直线PO的方程为2x+y=0时，|PM|最小，
此时P点即为两直线的交点，得P点坐标（- 
， 
）．
【解析】（1）将圆的一般方程变为标准方程，得到圆心坐标和半径，分切线过原点和不过原点设方程，由点到直线的距离等于半径列出等式，得到切线方程；（2）在直角△PMC中，根据勾股定理得出
，列出等式得到P点的轨迹方程，当直线PO垂直于直线2x-4y+3=0时，|PM|最小，联立解出交点坐标.
通城学典默写能手系列答案
【题目】一个容量为M的样本数据，其频率分布表如下．
（1）计算a,b的值;
（2）画出频率分布直方图；
（3）用频率分布直方图，求出总体的众数及平均数的估计值．
频率分布表
分组 | 频数 | 频率 | 频率/组距 |
(10,20] | 2 | 0.10 | 0.010 |
(20,30] | 3 | 0.15 | 0.015 |
(30,40] | 4 | 0.20 | 0.020 |
(40,50] | a | b | 0.025 |
(50,60] | 4 | 0.20 | 0.020 |
(60, 70] | 2 | 0.10 | 0.010 |
