题目内容
若函数 分别是
分别是 上的奇函数、偶函数,且满足
上的奇函数、偶函数,且满足 ,则有( ).
,则有( ).
 分别是
分别是 上的奇函数、偶函数,且满足
上的奇函数、偶函数,且满足 ,则有( ).
,则有( ).A. | B. |
C. | D. |
A
本题考查函数奇偶性的应用、方程思想。
由于函数 分别是
分别是 上的奇函数、偶函数,在
上的奇函数、偶函数,在 中,用
中,用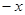 替换
替换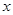 整理可得
整理可得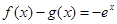 ,可解得
,可解得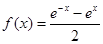 ,
,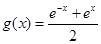 ,故
,故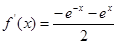 ,
,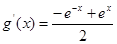 ,故
,故 ,选A。
,选A。
由于函数
 分别是
分别是 上的奇函数、偶函数,在
上的奇函数、偶函数,在 中,用
中,用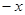 替换
替换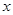 整理可得
整理可得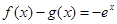 ,可解得
,可解得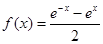 ,
,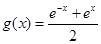 ,故
,故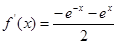 ,
,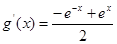 ,故
,故 ,选A。
,选A。
练习册系列答案
相关题目
题目内容
 分别是
分别是 上的奇函数、偶函数,且满足
上的奇函数、偶函数,且满足 ,则有( ).
,则有( ).A. | B. |
C. | D. |
 分别是
分别是 上的奇函数、偶函数,在
上的奇函数、偶函数,在 中,用
中,用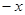 替换
替换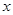 整理可得
整理可得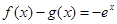 ,可解得
,可解得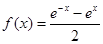 ,
,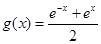 ,故
,故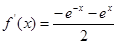 ,
,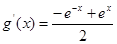 ,故
,故 ,选A。
,选A。