Question

【题目】已知函数f（x）是定义在R上的偶函数，已知x≥0时，f（x）=x2﹣2x．
（1）画出偶函数f（x）的图像的草图，并求函数f（x）的单调递增区间；
（2）当直线y=k（k∈R）与函数y=f（x）恰有4个交点时，求k的取值范围．

Answer 1

【答案】
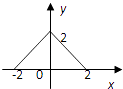
（1）解：画出f（x）的图像如下图：

由图像知，函数f（x）单调递增区间为[﹣1，0]，[1，+∞）

（2）解：由图像可知，当﹣1＜k＜0时，直线与函数y=f（x）的图像的交点个数为4；

∴k的取值范围为（﹣1，0）

【解析】（1）根据已知条件画出函数f（x）的图像，根据图像即可得到f（x）的单调递增区间；（2）通过图像即可得到k的取值范围．
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识，掌握在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇，以及对二次函数的性质的理解，了解当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减．