题目内容
一个多面体的三视图分别是正方形、等腰三角形和矩形, 其尺寸如图,则该多面体的体积为 
A. | B. |
C. | D. |
A
解析试题分析:观察三视图可知,这是一个横放的直三棱柱,底面为等腰三角形,底边长为6cm,底三角形高为4cm;直三棱柱的高为4cm,所以其体积为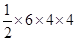 =
= ,
,
故选A。
考点:本题主要考查三视图及几何体的体积计算。
点评:基础题,认识几何体的几何特征是解题的关键。注意与常见几何体相联系。

练习册系列答案
相关题目
若某多面体的三视图如图所示,则此多面体的体积是( )
| A.2 | B.4 | C.6 | D.12 |
若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( ) 

A.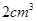 | B. |
C. | D. |
(理)球O与锐二面角α-l-β的两半平面相切,两切点间的距离为,O点到交线l的距离为2,则球O的表面积为( )
| A. | B.4π | C.12π | D.36π |
不共面的四点可以确定平面的个数为 ( )
| A.2个 | B.3个 | C.4个 | D.无法确定 |
一个棱锥的三视图如图,则该棱锥的表面积(单位:c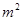 )为( )
)为( )
A.48+12 | B.48+24 | C.36+12 | D.36+24 |
若某空间几何体的三视图如图所示,则该几何体的体积是( )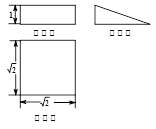
A. | B.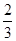 | C.1 | D. 2 |
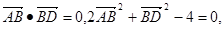 若将其沿BD折起,使平面ABD
若将其沿BD折起,使平面ABD 平面BDC则三棱锥A-BCD的外接球的表面积为:( )
平面BDC则三棱锥A-BCD的外接球的表面积为:( )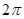



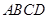 沿对角线
沿对角线 折成直二面角
折成直二面角 ,有如下四个结论:
,有如下四个结论: ⊥
⊥ 是等边三角形;③
是等边三角形;③ 与平面
与平面 所成的角为60°;④
所成的角为60°;④ 所成的角为60°.其中错误的结论是( )
所成的角为60°.其中错误的结论是( )