题目内容
将正方形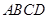 沿对角线
沿对角线 折成直二面角
折成直二面角 ,有如下四个结论:
,有如下四个结论:
① ⊥
⊥ ;②△
;②△ 是等边三角形;③
是等边三角形;③ 与平面
与平面 所成的角为60°;④
所成的角为60°;④ 与
与 所成的角为60°.其中错误的结论是( )
所成的角为60°.其中错误的结论是( )
| A.① | B.② | C.③ | D.④ |
C
解析试题分析:取BD的中点E,则AE⊥BD,CE⊥BD.∴BD⊥面AEC.∴BD⊥AC,故①正确.设正方形边长为a,则AD=DC=a,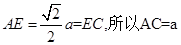 ,△ACD为等边三角形,故②正确。
,△ACD为等边三角形,故②正确。
∠ABD为AB与面BCD所成的角为45°,故③不正确。
以E为坐标原点,EC、ED、EA分别为x,y,z轴建立直角坐标系,则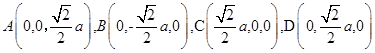 ,
,
所以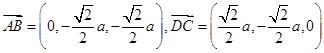 ,
,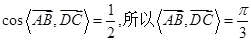 ,故④正确。
,故④正确。
考点:线面垂直的判定定理;直线与平面所成的角;异面直线所成的角。
点评:把一个平面图形折叠成一个几何体,再研究其性质,是考查空间想象能力的一种方法。我们要注意在折叠过程中那些关系发生改变,那些关系不改变。几何体的展开与折叠问题是考试的热点。本题根据已知条件将正方形ABCD沿对角线BD折成直二面角A-BD-C,结合立体几何求出相关直线与直线、直线与平面的夹角,及线段的长是关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
已知球的直径SC=4,A,B是该球球面上的两点,AB=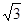 ,
,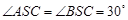 ,则棱锥S—ABC的体积为( )
,则棱锥S—ABC的体积为( )
A. | B.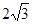 | C.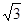 | D.1 |
一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形. 则该几何体的表面积为 ( )
| A.16 | B.48 |
| C.60 | D.96 |
若轴截面为正方形的圆柱的侧面积是 ,那么圆柱的体积等于
,那么圆柱的体积等于
A. | B. | C. | D. |
利用斜二侧画法画水平放置的平面图形的直观图,得到下列结论,其中正确的是( )
| A.正三角形的直观图仍然是正三角形. |
| B.平行四边形的直观图一定是平行四边形. |
| C.正方形的直观图是正方形. |
| D.圆的直观图是圆 |
如图是一个空间几何体的三视图,则该几何体的侧面积为
A.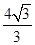 | B.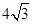 | C.8 | D.12 |