题目内容
【题目】已知f(x)=2ax﹣ ![]() +lnx在x=1与x=
+lnx在x=1与x= ![]() 处都取得极值. (Ⅰ) 求a,b的值;
处都取得极值. (Ⅰ) 求a,b的值;
(Ⅱ)设函数g(x)=x2﹣2mx+m,若对任意的x1∈[ ![]() ,2],总存在x2∈[
,2],总存在x2∈[ ![]() ,2],使得g(x1)≥f(x2)﹣lnx2 , 求实数m的取值范围.
,2],使得g(x1)≥f(x2)﹣lnx2 , 求实数m的取值范围.
【答案】解:(Ⅰ)∵ ![]() , ∵
, ∵ ![]() 在x=1与
在x=1与 ![]() 处都取得极值,
处都取得极值,
∴f'(1)=0, ![]() ,∴
,∴ ![]() ,解得
,解得 ![]() ,
,
当 ![]() 时,
时, 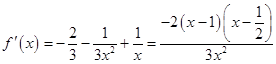 ,
,
所以函数f(x)在x=1与 ![]() 处都取得极值.
处都取得极值.
∴ ![]() ;
;
(Ⅱ)由(Ⅰ)知:函数 ![]() 在
在 ![]() 上递减,
上递减,
∴[f(x)﹣g(x)]min=﹣ ![]() +
+ ![]() =﹣
=﹣ ![]() ,
,
又函数g(x)=x2﹣2mx+m图象的对称轴是x=m,
①当 ![]() 时:
时: ![]() ,依题意有
,依题意有 ![]() 成立,∴
成立,∴ ![]() ;
;
②当 ![]() 时:
时: ![]() ,
,
∴ ![]() ,即6m2﹣6m﹣7≤0,解得:
,即6m2﹣6m﹣7≤0,解得: ![]() ,
,
又∵ ![]() ,∴
,∴ ![]() ;
;
③当m>2时,g(x)min=g(2)=4﹣3m,∴ ![]() ,解得
,解得 ![]() ,
,
又 m>2,∴m∈;
综上: ![]() ,
,
所以,实数m的取值范围为 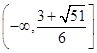
【解析】(Ⅰ)求导数f′(x),由f(x)在x=1与 ![]() 处都取得极值,得f'(1)=0,
处都取得极值,得f'(1)=0, ![]() ,得关于a,b的方程组,解出a,b,然后检验;(Ⅱ)对任意的
,得关于a,b的方程组,解出a,b,然后检验;(Ⅱ)对任意的 ![]() ,总存在
,总存在 ![]() ,使得g(x1)≥f(x2)﹣lnx2 , 等价于g(x)min≥[f(x)﹣lnx]min , 利用函数单调性易求[f(x)﹣lnx]min , 按照对称轴在区间[
,使得g(x1)≥f(x2)﹣lnx2 , 等价于g(x)min≥[f(x)﹣lnx]min , 利用函数单调性易求[f(x)﹣lnx]min , 按照对称轴在区间[ ![]() ,2]的左侧、内部、右侧三种情况进行讨论可求得g(x)min , 然后解不等式g(x)min≥[f(x)﹣lnx]min可得答案;
,2]的左侧、内部、右侧三种情况进行讨论可求得g(x)min , 然后解不等式g(x)min≥[f(x)﹣lnx]min可得答案;
【考点精析】本题主要考查了函数的极值和函数的最大(小)值与导数的相关知识点,需要掌握极值反映的是函数在某一点附近的大小情况;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.

【题目】已知两个函数f(x)和g(x)的定义域和值域都是集合{1,2,3},其定义如下表:则方程g(f(x))=x的解集为( )
x | 1 | 2 | 3 |
f(x) | 2 | 3 | 1 |
x | 1 | 2 | 3 |
g(x) | 3 | 2 | 1 |
A.{1}
B.{2}
C.{3}
D.
