题目内容
函数f(x)=ax2+(a-3)x+1在区间[-1,+∞)上是递减的,则实数a的取值范围是( )
| A.[-3,0) | B.(-∞,-3] |
| C.[-2,0] | D.[-3,0] |
D
解析

练习册系列答案
相关题目
下列各组函数表示同一函数的是( )
A. | B. |
C. | D. |
下列函数中,与函数 相同的是( )
相同的是( )
A. | B.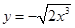 | C. | D. |
已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增.若实数a满足f(log2a)+f( a)≤2f(1),则a的取值范围是( )
a)≤2f(1),则a的取值范围是( )
| A.[1,2] | B. | C. | D.(0,2] |
设f(x)是连续的偶函数,且当x>0时是单调函数,则满足f(2x)=f(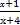 )的所有x之和为( )
)的所有x之和为( )
A.- | B.- | C.-8 | D.8 |
函数f(x)= +
+ 的定义域为( ).
的定义域为( ).
| A.(-3,0] | B.(-3,1] |
| C.(-∞,-3)∪(-3,0] | D.(-∞,-3)∪(-3,1] |
 中定义一种运算“
中定义一种运算“ ”,对任意
”,对任意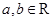 ,
, 为唯一确定的实数,且具有性质:
为唯一确定的实数,且具有性质: ,
, ;
;  .
. 的性质,有如下说法:①函数
的性质,有如下说法:①函数 的最小值为
的最小值为 ;②函数
;②函数 .
.


