题目内容
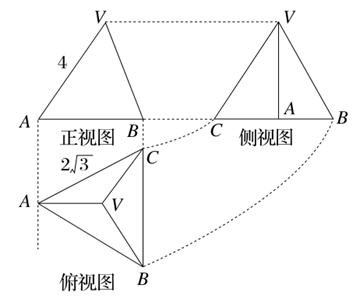
四面体 及其三视图如图所示,平行于棱
及其三视图如图所示,平行于棱 的平面分别交四面体的棱
的平面分别交四面体的棱 于点
于点 .
.
(1)求四面体 的体积;
的体积;
(2)证明:四边形 是矩形.
是矩形.
(1)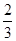 ;(2)证明见解析.
;(2)证明见解析.
解析试题分析:(1)由该四面体的三视图可知: ,
,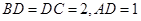 ,
,
所以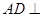 平面
平面 ,故四面体体积
,故四面体体积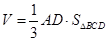 ,即可求出四面体
,即可求出四面体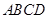 的体积.
的体积.
(2)由该四面体的三视图可知: ,
,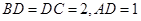
由题设,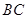 ∥面
∥面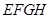 ,面
,面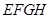
 面
面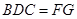 ,面
,面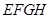
 面
面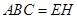 ,所以
,所以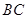 ∥
∥ ,
,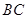 ∥
∥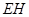 ,所以
,所以 ∥
∥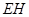 ,同理可得
,同理可得 ∥
∥ ,即得四边形
,即得四边形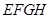 是平行四边形,同时可证
是平行四边形,同时可证 ,即证四边形
,即证四边形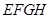 是矩形;
是矩形;
试题解析:
(1)由该四面体的三视图可知: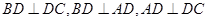 ,
,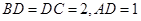
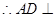 平面
平面
 四面体体积
四面体体积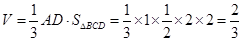
(2)由该四面体的三视图可知: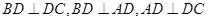 ,
,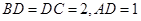
由题设,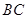 ∥面
∥面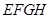
面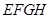
 面
面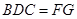
面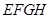
 面
面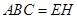
 ∥
∥ ,
,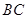 ∥
∥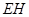 ,
, 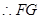 ∥
∥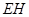 .
.
同理 ∥
∥ ,
, ∥
∥ ,
, 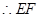 ∥
∥ .
. 四边形
四边形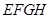 是平行四边形
是平行四边形
又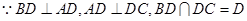
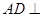 平面
平面
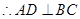
 ∥
∥ ,
, ∥
∥
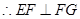
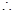 四边形
四边形 是矩形
是矩形
考点:四面体的体积;面面平行的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,侧棱垂直底面,
中,侧棱垂直底面, ,
, ,
, 是棱
是棱 的中点。
的中点。 ⊥平面
⊥平面
 ,求几何体
,求几何体 的体积。
的体积。
 及其三视图如图所示,过棱
及其三视图如图所示,过棱 的中点
的中点 作平行于
作平行于 ,
, 的平面分
的平面分 于点
于点 .
.
 是矩形;
是矩形; 的正弦值.
的正弦值. ,
, ,
, ,
, .又
.又 ,
, ,
, ,直线
,直线 与直线
与直线 所成的角为60°.
所成的角为60°. ;
; 的体积.
的体积.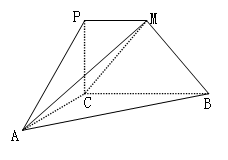


 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积. ,将其补成一个矩形,则根据矩形的对角线长可求得该直角三角形外接圆的半径为
,将其补成一个矩形,则根据矩形的对角线长可求得该直角三角形外接圆的半径为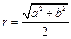 ”. 对于“若三棱锥三条侧棱两两垂直,侧棱长分别为
”. 对于“若三棱锥三条侧棱两两垂直,侧棱长分别为 ”,类比上述处理方法,可得该三棱锥的外接球半径为
”,类比上述处理方法,可得该三棱锥的外接球半径为 = ▲ .
= ▲ .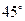 角的平面截球O的表面得到圆C.若圆C的面积等于
角的平面截球O的表面得到圆C.若圆C的面积等于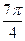 ,则球O的表面积等于 .
,则球O的表面积等于 .