题目内容
【题目】如图1,菱形![]() 中,
中,![]() ,
,![]() ,
,![]() 于
于![]() .将
.将![]() 沿
沿![]() 翻折到
翻折到![]() ,使
,使![]() ,如图2.
,如图2.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线A′E与平面A′BC所成角的正弦值;
(Ⅲ)设![]() 为线段
为线段![]() 上一点,若
上一点,若![]() 平面
平面![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)见解析;(Ⅱ)![]() ;(Ⅲ)1
;(Ⅲ)1
【解析】
(Ⅰ)证明DE⊥AE,DE⊥EB.A′E⊥DE.结合A′E⊥BE,证明A′E⊥平面BCDE.然后证明平面A′ED⊥平面BCDE;(Ⅱ)建立空间直角坐标系E﹣xyz,求出平面A′BC的法向量,利用空间向量的数量积求解直线A′E与平面A′BC所成角的正弦值;(Ⅲ)设![]() ,通过EF∥平面A′BC,所以
,通过EF∥平面A′BC,所以![]() ,求出m,然后推出结果即可.
,求出m,然后推出结果即可.
(Ⅰ)在菱形![]() 中,因为
中,因为![]() ,所以
,所以![]() ,
,![]() .
.
所以![]() .因为
.因为![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .因为
.因为![]() 平面
平面![]() ,
,
所以平面![]() ⊥平面
⊥平面![]() .
.
(Ⅱ)由(Ⅰ)知![]() ,
,![]() ,
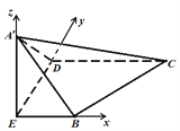
,![]() ,如图建立空间直角坐标系
,如图建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,由
,由
得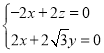 所以
所以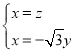 令
令![]() ,则
,则![]() .所以
.所以![]() .
.
所以![]() ,又
,又![]() ,
,![]() ,
,
所以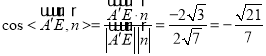 .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(Ⅲ)由(Ⅱ)可知,![]() ,
,![]()
设![]() ,则
,则![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() ,即
,即![]() .
.
所以![]() ,即
,即![]() .所以
.所以![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目