题目内容
【题目】已知![]() 的面积为
的面积为![]() ,且满足
,且满足![]() ,则边
,则边![]() 的最小值为_______.
的最小值为_______.
【答案】![]()
【解析】
将正切化成正余弦,化简得出b,c和sinA之间的关系,结合面积公式即可得出b2关于A的函数式,再根据A的范围计算b的最小值,即可得AC的最小值.
∵![]() ,∴
,∴![]() ,∴4cosAsinB+3cosBsinA=sinAsinB,
,∴4cosAsinB+3cosBsinA=sinAsinB,
∴3cosAsinB+3cosBsinA=sinAsinB﹣cosAsinB,
即3sin(A+B)=sinB(sinA﹣cosA),即3sinC=sinB(sinA﹣cosA),
∴3c=b(sinA﹣cosA),即c![]() ,
,
∵△ABC的面积S=![]() bcsinA=
bcsinA=![]()
=![]() (sin2A﹣cosAsinA)=
(sin2A﹣cosAsinA)=![]() (1﹣sin2A﹣cos2A)=
(1﹣sin2A﹣cos2A)=![]() ,
,
∴b2=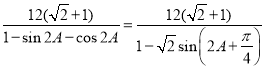 ,∵3c=b(sinA﹣cosA)>0,且0<A<π,
,∵3c=b(sinA﹣cosA)>0,且0<A<π,
∴![]() ,∴当
,∴当![]() 即A=
即A=![]() 时,b2取得最小值
时,b2取得最小值![]() =12,
=12,
∴b的最小值为![]() ,即AC最小值为
,即AC最小值为![]() .
.
故答案为:![]() .
.

【题目】某大型商场去年国庆期间累计生成![]() 万张购物单,从中随机抽出
万张购物单,从中随机抽出![]() 张,对每单消费金额进行统计得到下表:
张,对每单消费金额进行统计得到下表:
消费金额(单位:元) |
|
|
|
|
|
购物单张数 | 25 | 25 | 30 | 10 | 10 |
由于工作人员失误,后两栏数据已无法辨识,但当时记录表明,根据由以上数据绘制成的频率分布直方图所估计出的每单消费额的中位数与平均数恰好相等.用频率估计概率,完成下列问题:
(1)估计去年国庆期间该商场累计生成的购物单中,单笔消费额超过![]() 元的概率;
元的概率;
(2)为鼓励顾客消费,该商场打算在今年国庆期间进行促销活动,凡单笔消费超过![]() 元者,可抽奖一次,中一等奖、二等奖、三等奖的顾客可以分别获得价值
元者,可抽奖一次,中一等奖、二等奖、三等奖的顾客可以分别获得价值![]() 元、
元、![]() 元、
元、![]() 元的奖品.已知中奖率为
元的奖品.已知中奖率为![]() ,且一等奖、二等奖、三等奖的中奖率依次构成等比数列,其中一等奖的中奖率为
,且一等奖、二等奖、三等奖的中奖率依次构成等比数列,其中一等奖的中奖率为![]() .若今年国庆期间该商场的购物单数量比去年同期增长
.若今年国庆期间该商场的购物单数量比去年同期增长![]() ,式预测商场今年国庆期间采办奖品的开销.
,式预测商场今年国庆期间采办奖品的开销.
【题目】某公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间x与乘客等候人数y之间的关系,经过调查得到如下数据:
间隔时间x/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
与实际等候人数y的差,若差值的绝对值都不超过1,则称所求方程是“恰当回归方程”.
(1)从这6组数据中随机选取4组数据,求剩下的2组数据的间隔时间相邻的概率;
(2)若选取的是中间4组数据,求y关于x的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”.
,并判断此方程是否是“恰当回归方程”.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: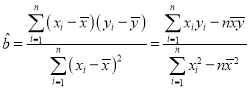 ,
,![]() .
.

