题目内容
(2013•宁波二模)设集合A={x,y|y=
},B={x,y|y=k(x-b)+1},若对任意0≤k≤1都有A∩B≠∅,则实数b的取值范围是( )
| 4-x2 |
分析:依题意,可作出集合A与集合B中曲线的图形,依题意,数形结合即可求得实数b的取值范围.
解答:解:∵集合A={(x,y)|y=
},B={(x,y)|y=k(x-b)+1},
当0≤k≤1时,都有A∩B≠∅,作图如下:
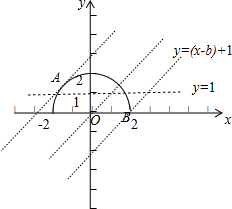
集合A中的曲线为以(0,0)为圆心,2为半径的上半圆,B中的点的集合为过(b,1)斜率为k的直线上的点,
由图知,当k=0时,显然A∩B≠∅,
当k=1,y=(x-b)+1经过点B(2,0)时,b=3;
当k=1,直线y=(x-b)+1与曲线y=
相切与点A时,由圆心(0,0)到该直线的距离d=
=2得:
b=1-2
或b=1+2
(舍).
∵0≤k≤1时,都有A∩B≠∅,
∴实数b的取值范围为:1-2
≤b≤3.
故选C.
| 4-x2 |
当0≤k≤1时,都有A∩B≠∅,作图如下:
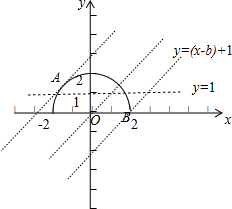
集合A中的曲线为以(0,0)为圆心,2为半径的上半圆,B中的点的集合为过(b,1)斜率为k的直线上的点,
由图知,当k=0时,显然A∩B≠∅,
当k=1,y=(x-b)+1经过点B(2,0)时,b=3;
当k=1,直线y=(x-b)+1与曲线y=
| 4-x2 |
| |1-b| | ||
|
b=1-2
| 2 |
| 2 |
∵0≤k≤1时,都有A∩B≠∅,
∴实数b的取值范围为:1-2
| 2 |
故选C.
点评:本题考查集合关系中的参数取值问题,考查数形结合思想的应用,考查作图与分析运算的能力,属于中档题.

练习册系列答案
相关题目
 (2013•宁波二模)如图是某学校抽取的n个学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第3个小组的频数为18,则的值n是
(2013•宁波二模)如图是某学校抽取的n个学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第3个小组的频数为18,则的值n是