题目内容
椭圆C: 的左右焦点分别为
的左右焦点分别为 ,若椭圆C上恰好有6个不同的点
,若椭圆C上恰好有6个不同的点 ,使得
,使得 为等腰三角形,则椭圆C的离心率取值范围是( )
为等腰三角形,则椭圆C的离心率取值范围是( )
 的左右焦点分别为
的左右焦点分别为 ,若椭圆C上恰好有6个不同的点
,若椭圆C上恰好有6个不同的点 ,使得
,使得 为等腰三角形,则椭圆C的离心率取值范围是( )
为等腰三角形,则椭圆C的离心率取值范围是( )A. | B. | C. | D. |
D
试题分析:6个不同的点有两个为短轴的两个端点,另外4个分别在第一、二、三、四象限,且上下对称左右对称。不妨设
 在第一象限,
在第一象限,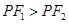 ,当
,当 时,
时,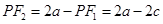 ,即
,即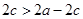 ,解得
,解得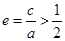 ,又因为
,又因为 ,所以
,所以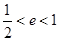 ;当
;当 时,
时,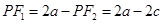 ,即
,即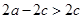 且
且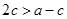 ,解得
,解得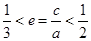 ,即
,即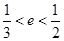 。综上可得
。综上可得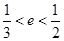 或
或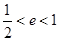 。故D正确。
。故D正确。
练习册系列答案
相关题目
 的焦点在
的焦点在 轴上,
轴上,  分别是椭圆的左、右焦点,点
分别是椭圆的左、右焦点,点 是椭圆在第一象限内的点,直线
是椭圆在第一象限内的点,直线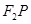 交
交 轴于点
轴于点 ,
, 时,
时, 的离心率为
的离心率为 ,求椭圆
,求椭圆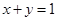 上时,求直线
上时,求直线 与
与 的夹角;
的夹角; 时,若总有
时,若总有 ,猜想:当
,猜想:当 变化时,点
变化时,点 是否在某定直线上,若是写出该直线方程(不必求解过程).
是否在某定直线上,若是写出该直线方程(不必求解过程). 的离心率是
的离心率是 ,则
,则 的值为 .
的值为 . .
. ,点B在椭圆C上,且
,点B在椭圆C上,且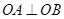 ,求线段AB长度的最小值.
,求线段AB长度的最小值.
 的左、右焦点为
的左、右焦点为 、
、 ,离心率为
,离心率为 ,过
,过 交C于A、B两点,若
交C于A、B两点,若 的周长为
的周长为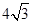 ,则C的方程为
,则C的方程为 B.
B. C.
C. D.
D.
 :
: ,过点
,过点
 的直线与椭圆
的直线与椭圆 、
、 两点,若点
两点,若点 的中点,则直线
的中点,则直线 ,长轴长为6,
,长轴长为6, +
+ =1(a>b>0)的左、右焦点分别为F1,F2.点P(a,b)满足|PF2|=|F1F2|.
=1(a>b>0)的左、右焦点分别为F1,F2.点P(a,b)满足|PF2|=|F1F2|. =16相交于M,N两点,且|MN|=
=16相交于M,N两点,且|MN|= |AB|,求椭圆的方程.
|AB|,求椭圆的方程. 的焦点恰好与椭圆
的焦点恰好与椭圆 的一个焦点重合,则
的一个焦点重合,则 ( )
( )