题目内容
（2009•台州一模）已知双曲线x2-y2=4a（a∈R，a≠0）的右焦点是椭圆
+
=1的一个顶点，则a=
| x2 |
| 16 |
| y2 |
| 9 |
2
2
．分析：先岔气椭圆
+
=1的方程得出其右顶点，从而由题意知双曲线x2-y2=4a（a∈R，a≠0）的右焦点是（4，0），再根据双曲线的几何性质得出关于字母a的方程，即可求出a的值．
| x2 |
| 16 |
| y2 |
| 9 |
解答：解：椭圆
+
=1的右顶点为（4，0），
故双曲线x2-y2=4a（a∈R，a≠0）的右焦点是（4，0），
∴4a+4a=42，∴a=2．
故答案为：2．
| x2 |
| 16 |
| y2 |
| 9 |
故双曲线x2-y2=4a（a∈R，a≠0）的右焦点是（4，0），
∴4a+4a=42，∴a=2．
故答案为：2．
点评：本题考查了双曲线的简单性质，考查了椭圆的简单性质，此题是基础题．
练习册系列答案
名校课堂系列答案
相关题目
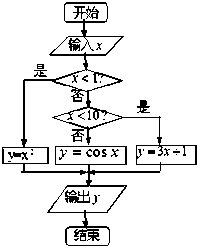（2009•台州一模）根据右边程序框图，若输出y的值是4，则输入的实数x=