题目内容
（2009•台州一模）已知向量
=（sinx，1），
=（t，x），若函数f（x）=
•
在区间[0，
]上是增函数，则实数t的取值范围是
| a |
| b |
| a |
| b |
| π |
| 2 |
[-1，+∞）
[-1，+∞）
．分析：根据平面向量的数量积运算，可得f（x）=tsinx+x在区间[0，
]上是增函数．由导数与函数单调性的关系，得不等式
f'（x）≥0即tcosx+1≥0区间[0，
]上恒成立，结合此时cosx的值域即可得到实数t的取值范围．
| π |
| 2 |
f'（x）≥0即tcosx+1≥0区间[0，
| π |
| 2 |
解答：解：∵
=（sinx，1），
=（t，x），
∴
•
=sinx•t+1•x=tsinx+x，
由此可得f（x）=
•
=tsinx+x，在区间[0，
]上是增函数，
∴f'（x）≥0区间[0，
]上恒成立，
∵对函数f（x）求导数，得f'（x）=tcosx+1，
∴不等式tcosx+1≥0区间[0，
]上恒成立，
结合在区间[0，
]上0≤cosx≤1，可得t≥-1
即实数t的取值范围是：[-1，+∞）
故答案为：[-1，+∞）
| a |
| b |
∴
| a |
| b |
由此可得f（x）=
| a |
| b |
| π |
| 2 |
∴f'（x）≥0区间[0，
| π |
| 2 |
∵对函数f（x）求导数，得f'（x）=tcosx+1，
∴不等式tcosx+1≥0区间[0，
| π |
| 2 |
结合在区间[0，
| π |
| 2 |
即实数t的取值范围是：[-1，+∞）
故答案为：[-1，+∞）
点评：本题以向量数量积运算为载体，求函数恒成立时实数t的取值范围，着重考查了运用导数研究函数的单调性、不等式恒成立等知识，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
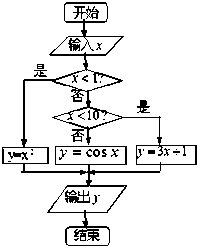（2009•台州一模）根据右边程序框图，若输出y的值是4，则输入的实数x=