题目内容
(2009•台州一模)已知点B(0,t),点C(0,t-4)(其中0<t<4),直线PB、PC都是圆M:(x-1)2+y2=1的切线.
(Ⅰ)若△PBC面积等于6,求过点P的抛物线y2=2px(p>0)的方程;
(Ⅱ)若点P在y轴右边,求△PBC面积的最小值.
(Ⅰ)若△PBC面积等于6,求过点P的抛物线y2=2px(p>0)的方程;
(Ⅱ)若点P在y轴右边,求△PBC面积的最小值.
分析:(Ⅰ)利用△PBC面积等于6,确定P的坐标,结合直线PB与圆M相切,即可求过点P的抛物线y2=2px(p>0)的方程;
(Ⅱ)确定PB,PC的方程,求出P的横坐标,表示出△PBC面积,即可求得最小值.
(Ⅱ)确定PB,PC的方程,求出P的横坐标,表示出△PBC面积,即可求得最小值.
解答:解:(Ⅰ)设P(xp,yp),由已知xp>0,
∵S△PBC=
×4×xp=6,∴xp=3,∴P(3,±
),(2分)
设直线PB与圆M切于点A,
∵S△PBC=
×(4+4+2PA)×1=6,∴PA=2,
∵M(1,0)∴PM=
,∴PM=
=
,
∴p=
,∴y2=
x(6分)
(Ⅱ)∵点 B(0,t),点C(0,t-4),(7分)
∴两条切线方程为:PB:y=
x+t,PC:y=
x+t-4,(9分)
∴
xp+t=
xp+t-4,
∴xp=
,
∵0<t<4,∴xp<0或xp≥
,
∵xp>0,∴xp≥
,(13分)
∴S△PBC=
×4×xp≥
,
又∵t=2时,S△PBC=
,∴△PBC面积的最小值为
(15分)
∵S△PBC=
| 1 |
| 2 |
| 6p |
设直线PB与圆M切于点A,
∵S△PBC=
| 1 |
| 2 |
∵M(1,0)∴PM=
| 5 |
| 4+6p |
| 5 |
∴p=
| 1 |
| 6 |
| 1 |
| 3 |
(Ⅱ)∵点 B(0,t),点C(0,t-4),(7分)
∴两条切线方程为:PB:y=
| 1-t2 |
| 2t |
| -t2+8t-15 |
| 2t-8 |
∴
| 1-t2 |
| 2t |
| -t2+8t-15 |
| 2t-8 |
∴xp=
| 2t2-8t |
| t2-4t+1 |
∵0<t<4,∴xp<0或xp≥
| 8 |
| 3 |
∵xp>0,∴xp≥
| 8 |
| 3 |
∴S△PBC=
| 1 |
| 2 |
| 16 |
| 3 |
又∵t=2时,S△PBC=
| 16 |
| 3 |
| 16 |
| 3 |
点评:本题考查抛物线方程,考查直线与圆的位置关系,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
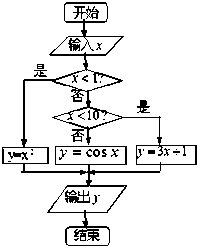 (2009•台州一模)根据右边程序框图,若输出y的值是4,则输入的实数x=
(2009•台州一模)根据右边程序框图,若输出y的值是4,则输入的实数x=