题目内容
（2009•台州一模）已知点（3，1）和原点（0，0）在直线3x-ay+1=0的两侧，则实数a的取值范围是（ ）
分析：因为点（3，1）和原点（0，0）在直线3x-ay+1=0的两侧，所以（3×0-a×0+1）•（3×3-a×1+1）＜0，由此能求出a的取值范围．
解答：解：因为点（3，1）和原点（0，0）在直线3x-ay+1=0的两侧，
所以（3×0-a×0+1）•（3×3-a×1+1）＜0，解得a＞10，
故选B．
所以（3×0-a×0+1）•（3×3-a×1+1）＜0，解得a＞10，
故选B．
点评：本题考查二元一次不等式的几何意义，解题时要认真审题，注意公式的灵活运用．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
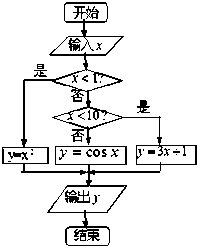（2009•台州一模）根据右边程序框图，若输出y的值是4，则输入的实数x=