题目内容
3.已知O为坐标原点,椭圆$\frac{x^2}{2}+{y^2}$=1的左、右焦点分别为F1,F2,点P为直线l:x+y=2上且不在x轴上的任意一点.(Ⅰ)求△F1PF2周长的最小值;
(Ⅱ)设直线PF1和PF2的斜率分别为k1,k2,直线PF1和PF2与椭圆的交点分别为A,B和C,D.
①证明:$\frac{1}{k_1}-\frac{3}{k_2}$=2;
②当直线OA,OB,OC,OD的斜率之和为0时,求直线l上点P的坐标.
分析 (Ⅰ)过F2作直线x+y=2的对称点M,由对称知识,可得M的坐标,即有|PF1|+|PF2|的最小值为|MF1|,可得△F1PF2周长的最小值;
(Ⅱ)①把直线PF1、PF2的方程联立求得交点的坐标的表达式,代入直线x+y=2上,整理求得$\frac{1}{k_1}-\frac{3}{k_2}$=2,原式得证;
②设出A,B,C,D的坐标,联立直线PF1和椭圆的方程根据韦达定理表示出xA+xB和xAxB,进而可求得直线OA,OB斜率的和与CO,OD斜率的和,由kOA+kOB+kOC+kOD=0推断出k1+k2=0或k1k2=1,分别讨论求得p.
解答 解:(Ⅰ)过F2作直线x+y=2的对称点M,设M(m,n),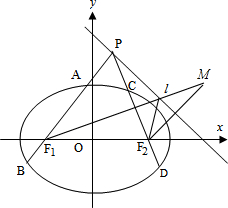
椭圆$\frac{x^2}{2}+{y^2}$=1的a=$\sqrt{2}$,b=1,c=1,
即有F1(-1,0)、F2(1,0),
可得$\left\{\begin{array}{l}{\frac{1}{2}(m+1)+\frac{1}{2}n=2}\\{\frac{n}{m-1}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=2}\\{n=1}\end{array}\right.$,
即为M(2,1),则|PF1|+|PF2|的最小值为
|MF1|=$\sqrt{(2+1)^{2}+(1-0)^{2}}$=$\sqrt{10}$,
则△F1PF2周长的最小值为|F1F2|+|MF1|=2+$\sqrt{10}$;
(Ⅱ)①由于F1(-1,0)、F2(1,0),
PF1,PF2的斜率分别是k1,k2,且点P不在x轴上,
所以k1≠k2,k1≠0,k2≠0.
又直线PF1、PF2的方程分别为y=k1(x+1),y=k2(x-1),
联立方程解得$\left\{\begin{array}{l}{x=\frac{{k}_{1}+{k}_{2}}{{k}_{2}-{k}_{1}}}\\{y=\frac{2{k}_{1}{k}_{2}}{{k}_{2}-{k}_{1}}}\end{array}\right.$,
所以P($\frac{{k}_{1}+{k}_{2}}{{k}_{2}-{k}_{1}}$,$\frac{2{k}_{1}{k}_{2}}{{k}_{2}-{k}_{1}}$),由于点P在直线x+y=2上,
所以$\frac{{k}_{1}+{k}_{2}}{{k}_{2}-{k}_{1}}$+$\frac{2{k}_{1}{k}_{2}}{{k}_{2}-{k}_{1}}$=2,即2k1k2+3k1-k2=0,
故$\frac{1}{{k}_{1}}$-$\frac{3}{{k}_{2}}$=2;
②由$\left\{{\begin{array}{l}{y={k_1}(x+1)}\\{{x^2}+2{y^2}=2}\end{array}}\right.$,得$(1+2k_1^2){x^2}+4k_1^2x+2k_1^2-2=0$,
即有$\left\{{\begin{array}{l}{{x_1}+{x_2}=\frac{-4k_1^2}{1+2k_1^2}}\\{{x_1}{x_2}=\frac{2(k_1^2-1)}{1+2k_1^2}}\end{array}}\right.$,${k_{OA}}+{k_{OB}}=\frac{y_1}{x_1}+\frac{y_2}{x_2}=\frac{{{k_1}({x_1}+1)}}{x_1}+\frac{{{k_1}({x_2}+1)}}{x_2}={k_1}(2+\frac{1}{x_1}+\frac{1}{x_2})={k_1}(2+\frac{{{x_1}+{x_2}}}{{{x_1}{x_2}}})=\frac{{2{k_1}}}{1-k_1^2}$,
同样可算得,kOC+kOD=$\frac{2{k}_{2}}{1-{{k}_{2}}^{2}}$,
由kOA+kOB+kOC+kOD=0,得$\frac{{2{k_1}}}{k_1^2-1}+\frac{{2{k_2}}}{k_2^2-1}=0$,
整理得(k1+k2)(k1k2-1)=0,即k1+k2=0或k1k2=1,
又因为$\frac{1}{k_1}-\frac{3}{k_2}=2$,由$\left\{{\begin{array}{l}{{k_1}+{k_2}=0}\\{\frac{1}{k_1}-\frac{3}{k_2}=2}\end{array}}\right.,\left\{{\begin{array}{l}{{k_1}=2}\\{{k_2}=-2}\end{array}}\right.,P(0,2)$,
由$\left\{\begin{array}{l}{{k}_{1}{k}_{2}=1}\\{\frac{1}{{k}_{1}}-\frac{3}{{k}_{2}}=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{{k}_{1}=-1}\\{{k}_{2}=-1}\end{array}\right.$(舍)或$\left\{{\begin{array}{l}{{k_1}=\frac{1}{3}}\\{{k_2}=3}\end{array}}\right.,P(\frac{5}{4},\frac{3}{4})$,
综上可得,P(0,2)或$P(\frac{5}{4},\frac{3}{4})$.
点评 本题主要考查了直线与椭圆的关系的综合问题,椭圆的简单性质.考查了学生综合推理能力,基本计算能力.

 阅读快车系列答案
阅读快车系列答案| A. | $y=x+\frac{1}{x}$ | B. | y=xsinx+cosx | C. | $y={e^x}-\frac{1}{e^x}$ | D. | $y=ln\frac{1-x}{1+x}$ |
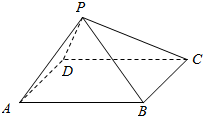 如图,在四棱锥P-ABCD中,有同学说平面PAD∩平面PBC=P,这句话对吗?请说明理由.
如图,在四棱锥P-ABCD中,有同学说平面PAD∩平面PBC=P,这句话对吗?请说明理由. 如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC,F为CE上的点,且BF⊥平面ACE.
如图所示,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC,F为CE上的点,且BF⊥平面ACE.