题目内容
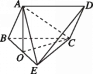
【题目】如图所示,在四棱锥E-ABCD中,四边形ABCD是平行四边形,△BCE是等边三角形,△ABE是等腰直角三角形,∠BAE=90°,且AC=BC.

(1)证明:平面ABE⊥平面BCE;
(2)求二面角A-DE-C的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)证明:设O为BE的中点,连接AO,CO,证得AO⊥BE,CO⊥BE和AO⊥CO,利用面面垂直的判定定理,即可证明;
(2)由(1)可知AO,BE,CO两两垂直,以O为坐标原点,OE,OC,OA分别为x,y,z轴建立空间直角坐标系,分别求解平面ADE和平面DEC的一个法向量,利用向量的夹角公式,即可求解.
(1)证明:设O为BE的中点,连接AO,CO,易知AO⊥BE,CO⊥BE.设AC=BC=2,则AO=1,CO=![]() ,可得AO2+CO2=AC2,所以AO⊥CO.又AO∩BE=O,所以CO⊥平面ABE.
,可得AO2+CO2=AC2,所以AO⊥CO.又AO∩BE=O,所以CO⊥平面ABE.
又CO平面BCE,故平面ABE⊥平面BCE.
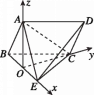
(2)由(1)可知AO,BE,CO两两垂直,
设OE=1,以O为坐标原点,OE,OC,OA分别为x,y,z轴建立如图所示的空间直角坐标系O-xyz,则A(0,0,1),E(1,0,0),C(0,![]() ,0),易得D(1,
,0),易得D(1,![]() ,1),故
,1),故![]() =(1,
=(1,![]() ,0),
,0),![]() =(1,0,-1),
=(1,0,-1),
![]() =(-1,
=(-1,![]() ,0),
,0),![]() =(1,0,1).设n=(x1,y1,z1)是平面ADE的法向量,则
=(1,0,1).设n=(x1,y1,z1)是平面ADE的法向量,则![]() 即
即![]() 令y1=1,可得n=(-
令y1=1,可得n=(-![]() ,1,-
,1,-![]() ).设m=(x2,y2,z2)是平面DEC的法向量,则
).设m=(x2,y2,z2)是平面DEC的法向量,则![]() 即
即![]() 令y2=1,可得m=(
令y2=1,可得m=(![]() ,1,-
,1,-![]() ),则cos<n,m>=
),则cos<n,m>=![]() =.
=.
易知二面角A-DE-C为锐角,所以二面角A-DE-C的余弦值为.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

