题目内容
已知椭圆C:的长轴长为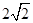 ,离心率
,离心率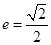 .
.
Ⅰ)求椭圆C的标准方程;
Ⅱ)若过点B(2,0)的直线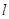 (斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且
(斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且 OBE与
OBE与 OBF的面积之比为
OBF的面积之比为 ,求直线
,求直线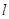 的方程.
的方程.
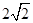 ,离心率
,离心率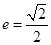 .
.Ⅰ)求椭圆C的标准方程;
Ⅱ)若过点B(2,0)的直线
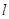 (斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且
(斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且 OBE与
OBE与 OBF的面积之比为
OBF的面积之比为 ,求直线
,求直线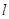 的方程.
的方程.(1)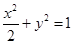 (2)
(2)
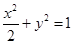 (2)
(2)
试题分析:解:(I)椭圆C的方程为
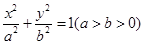 ,由已知得
,由已知得解得
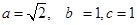 ∴所求椭圆的方程为
∴所求椭圆的方程为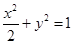 .
.(II)由题意知
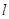 的斜率存在且不为零,
的斜率存在且不为零,设
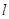 方程为
方程为 ①,将①代入
①,将①代入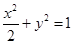 ,整理得
,整理得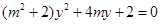 ,由
,由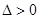 得
得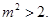
设
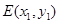 ,
, ,则
,则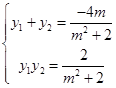 ②.
②. 由已知,
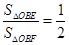 , 则
, 则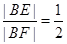
由此可知,
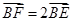 ,即
,即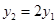 . 代入②得,,消去
. 代入②得,,消去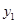 得
得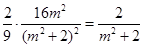 解得,
解得,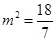 ,满足
,满足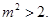 即
即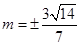 .
. 所以,所求直线
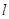 的方程为
的方程为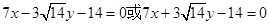 .
. 点评:主要是考查了椭圆的方程与性质,以及直线与椭圆的位置关系的运用,属于中档题。

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
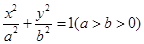 过点
过点 ,其长轴、焦距和短轴的长的平方依次成等差数列.
,其长轴、焦距和短轴的长的平方依次成等差数列. 轴正半轴、
轴正半轴、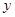 轴分别交于点
轴分别交于点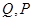 ,与椭圆分别交于点
,与椭圆分别交于点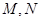 ,各点均不重合,且满足
,各点均不重合,且满足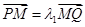 ,
,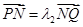 . 当
. 当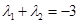 时,试证明直线过定点.过定点(1,0)
时,试证明直线过定点.过定点(1,0)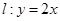 上一点
上一点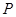 作圆
作圆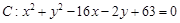 的切线
的切线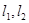 ,若
,若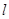 对称,则点
对称,则点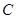 的距离为 .
的距离为 .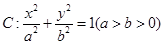 的左焦点为
的左焦点为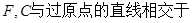

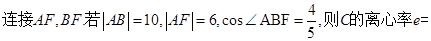 .
.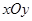 中,直线
中,直线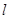 的方程为
的方程为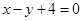 ,曲线
,曲线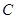 的参数方程为
的参数方程为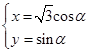 (
(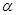 为参数).
为参数).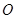 为极点,以
为极点,以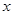 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点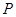 的极坐标为(4,
的极坐标为(4,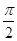 ),判断点
),判断点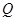 是曲线
是曲线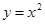 上的一动点
上的一动点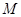 到直线
到直线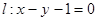 距离的最小值是 ( )
距离的最小值是 ( )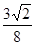
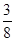

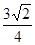
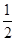 ,短轴长为4
,短轴长为4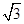 .
.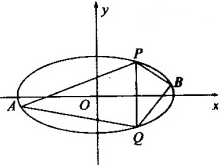
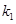 ,直线PB的斜率为
,直线PB的斜率为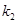 ,判断
,判断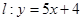 是曲线
是曲线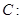
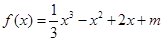 的一条切线,
的一条切线,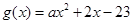 .
. 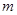 的值;
的值;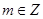 时,存在
时,存在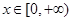
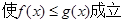 ,求实数
,求实数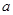 的取值范围.
的取值范围.