题目内容
设函数 (1)当
(1)当 时,求
时,求 的最大值;(2)令
的最大值;(2)令 ,(
,( ),其图象上任意一点
),其图象上任意一点 处切线的斜率
处切线的斜率 ≤
≤ 恒成立,求实数
恒成立,求实数 的取值范围;(3)当
的取值范围;(3)当 ,
, ,方程
,方程 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值.
(1) 的极大值为
的极大值为 ,此即为最大值;(2)
,此即为最大值;(2) ≥
≥ ;(3)
;(3) .
.
解析试题分析:(1)依题意,知 的定义域为(0,+∞),当
的定义域为(0,+∞),当 时,
时, ,
, (2′)令
(2′)令 =0, 解得
=0, 解得 .(∵
.(∵ )
)
因为当 时,
时, ,此时
,此时 单调递增;当
单调递增;当 时,
时, ,此时
,此时 单调递减。所以
单调递减。所以 的极大值为
的极大值为 ,此即为最大值 4分
,此即为最大值 4分
(2)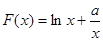 ,
, ,则有
,则有 ≤
≤ ,在
,在 上恒成立,
上恒成立,
所以 ≥
≥ ,
, (8′)当
(8′)当 时,
时, 取得最大值
取得最大值 ,所以
,所以 ≥
≥ 8分
8分
(3)因为方程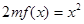 有唯一实数解,所以
有唯一实数解,所以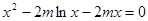 有唯一实数解,
有唯一实数解,
设 ,则
,则 .令
.令 ,
,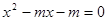 .
.
因为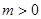 ,
, ,所以
,所以 (舍去),
(舍去), ,
,
当 时,
时, ,
, 在(0,
在(0, )上单调递减,当
)上单调递减,当 时,
时, ,
, 在(
在( ,+∞)单调递增 当
,+∞)单调递增 当 时,
时,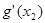 =0,
=0, 取最小值
取最小值 则
则 既
既 所以
所以 ,因为
,因为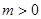 ,所以
,所以 (*)设函数
(*)设函数 ,因为当
,因为当 时,
时, 是增函数,所以
是增函数,所以 至多有一解.因为
至多有一解.因为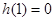 ,所以方程(*)的解为
,所以方程(*)的解为 ,即
,即 ,解得
,解得 . 12分
. 12分
考点:导数的几何意义,直线方程,利用导数研究函数的极值(最值),不等式恒成立问题。
点评:典型题,切线的斜率,等于在切点的导函数值。利用导数研究函数的极值,一般遵循“求导数、求驻点、研究导数的正负、确定极值”,利用“表解法”,清晰易懂。不等式恒成立问题,往往通过构造函数,通过研究函数的最值确定参数的范围。

练习册系列答案
相关题目

 的单调性;
的单调性; 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为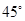 ,对于任意的
,对于任意的 ,函数
,函数 在区间
在区间  上总不是单调函数,
上总不是单调函数, 的取值范围;
的取值范围;

 的单调区间;
的单调区间; 上的最值.
上的最值. 在x=
在x= 与x =l时都取得极值
与x =l时都取得极值 在
在 时有极大值6,在
时有极大值6,在 时有极小值,求
时有极小值,求 的值;并求
的值;并求 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.
 在
在 和
和 处的切线互相平行,求
处的切线互相平行,求 的值及函数
的值及函数 的单调区间;
的单调区间; ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求实数
,求实数 ,其中
,其中 .
. 恒成立,求
恒成立,求 的取值范围;
的取值范围; 的图像上取定两点
的图像上取定两点 ,记直线
,记直线 的斜率为
的斜率为 ,证明:存在
,证明:存在 ,使
,使 成立.
成立. ,试比较
,试比较 与
与 的大小;
的大小; ,使得
,使得 对任意大于
对任意大于 的自然数
的自然数 都成立?若存在,试求出
都成立?若存在,试求出 的值并证明你的结论;若不存在,请说明理由。
的值并证明你的结论;若不存在,请说明理由。