题目内容
设函数f(x)=(1+x)2-2ln (1+x).
(1)求函数f(x)的单调区间;
(2)若关于x的方程f(x)=x2+x+a在[0,2]上恰有两个相异实根,求实数a的取值范围.
(1)f(x)的递增区间是(0,+∞),递减区间是(-1,0).
(2)(2-2ln 2,3-2ln 3].
解析试题分析:解 (1)函数的定义域为(-1,+∞),
因为f(x)=(1+x)2-2ln(1+x),
所以f′(x)=2 =
= ,
,
由f′(x)>0,得x>0;由f′(x)<0,得-1<x<0,
所以,f(x)的递增区间是(0,+∞),递减区间是(-1,0).
(2)方程f(x)=x2+x+a,即x-a+1-2ln(1+x)=0,
记g(x)=x-a+1-2ln(1+x)(x>-1),
则g′(x)=1- =
= ,
,
由g′(x)>0,得x>1;
由g′(x)<0,得-1<x<1.
所以g(x)在[0,1]上单调递减,在[1,2]上单调递增.
为使f(x)=x2+x+a在[0,2]上恰有两个相异的实根,
只须g(x)=0在[0,1)和(1,2]上各有一个实根,
于是有 即
即
解得2-2ln 2<a≤3-2ln 3,
故实数a的取值范围是(2-2ln 2,3-2ln 3].
考点:导数的运用,以及函数与方程
点评:解决的关键是根据导数判定函数单调性,以及函数的零点问题,属于中档题。

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 (1)当
(1)当 时,求
时,求 的最大值;(2)令
的最大值;(2)令 ,(
,( ),其图象上任意一点
),其图象上任意一点 处切线的斜率
处切线的斜率 ≤
≤ 恒成立,求实数
恒成立,求实数 的取值范围;(3)当
的取值范围;(3)当 ,
, ,方程
,方程 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值.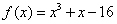 .
.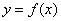 在点
在点 处的切线方程;
处的切线方程; 为曲线
为曲线 ;
; 在
在 上单调递增,在
上单调递增,在 上单调递减,在
上单调递减,在 上单调递增,求实数
上单调递增,求实数 的值;
的值; 时,求证:当
时,求证:当 时,
时,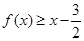 .
. 为偶函数,曲线
为偶函数,曲线 过点(2,5),
过点(2,5),  .
. 有斜率为0的切线,求实数
有斜率为0的切线,求实数 的取值范围;
的取值范围; 时函数
时函数 ,其中
,其中 。
。 有极值
有极值 ,求
,求 的值;
的值; 在区间
在区间 上为增函数,求
上为增函数,求
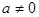 ,函数
,函数 .
. 有极大值32,求实数
有极大值32,求实数 的值;
的值; ,不等式
,不等式 恒成立,求实数
恒成立,求实数 在点
在点 处的切线与x轴交点的横坐标为an.
处的切线与x轴交点的横坐标为an. ,求数到
,求数到 的前n项和Sn.
的前n项和Sn. 为常数,已知函数
为常数,已知函数 在区间
在区间 上是增函数,
上是增函数,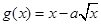 在区间
在区间 上是减函数.
上是减函数. 为函数
为函数 的图像上任意一点,求点
的图像上任意一点,求点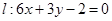 的距离的最小值;
的距离的最小值;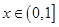 且
且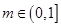 ,
, 恒成立,求实数
恒成立,求实数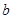 的取值范围.
的取值范围.