Question

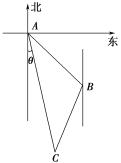
【题目】如图，甲船在A处，乙船在A处的南偏东45°方向，距A有9海里的B处，并以20海里每小时的速度沿南偏西15°方向行驶，若甲船沿南偏东θ度的方向，并以28海里每小时的速度行驶，恰能在C处追上乙船．问用多少小时追上乙船，并求sin θ的值．(结果保留根号，无需求近似值)

Answer 1

【答案】小时；

【解析】

设用t小时,甲船追上乙船,且在C处相遇,

则在△ABC中,AC＝28t,BC＝20t,AB＝9,

∠ABC＝180°－15°－45°＝120°,

由余弦定理得, ,

即128t2－60t－27＝0,

解得或(舍去),

∴AC＝21(海里),BC＝15(海里).

根据正弦定理,

得,

则.

又∠ABC＝120°,∠BAC为锐角,∴θ＝45°－∠BAC,

sin θ＝sin(45°－∠BAC)＝sin 45°cos∠BAC－cos 45°sin ∠BAC＝.