题目内容

已知
3x-y-3≤0
4x+y+3≥0
2x-3y+5≥0
，则z=|2x+y+5|的最大值与最小值的差为（　　）
A．8B．2C．10D．5
由题意，作出
3x-y-3≤0
4x+y+3≥0
2x-3y+5≥0
对应的可行域，如图，其中三个角点的坐标分别为A（2，3），B（-1，1），C（0，-3）．
对于z=|2x+y+5|在三个角点的取值情况如下：
在A（2，3）处时，z=12，
在B（-1，1）处时，z=4，
在C（0，-3）处时，z=2，
通过平移直线2x+y=0可知，z=|2x+y+5|的最大值与最小值必定在角点处取得，
故z=|2x+y+5|的最大值与最小值分别为12，2．
所以z=|2x+y+5|的最大值与最小值的差为10．
故选C．
练习册系列答案
相关题目
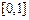在区间上任取两个数，则方程没有实根的概率为       .
已知变量x、y满足条件则的最大值是(     )
A．2B．5C．6D．8
某企业生产甲、乙两种产品，已知生产每吨甲产品要用3t原料A，2t天然气B；生产每吨乙产品要用1t原料A，3t天然气B，销售每吨甲产品可获得利润5万元，销售每吨乙产品可获得利润3万元．若该企业在一个生产周期内消耗的原料A不超过13t，B不超过18t，则该企业可获得最大利润为______万元．
已知关于x的二次函数f（x）=ax2-4bx+1
（Ⅰ）设集合P={1，2，3}，集合Q={-1，1，2，3，4}，从集合P中随机取一个数作为a，从集合Q中随机取一个数作为b，求函数f（x）在区间[1，+∞）上是增函数的概率；
（Ⅱ）设点（a，b）是区域
x+y-8≤0
x＞0
y＞0
内的随机点，求函数f（x）在区间[1，+∞）上是增函数的概率．
已知实数x，y满足不等式组
x≥0
y≥0
x+y≤1
，则x-y的最大值为______．
已知实数x，y满足不等式组
x+3y-3≥0
2x-y-3≤0
x-y+1≥0
，则
y-1
x+1
的取值范围是______．
已知变量x，y满足
2x-y≤0
x-3y+5≥0
x≥0
，则z=x-y+5的最大值为（　　）
A．4B．
10
3
C．2D．5
已知约束条件
x+2y≤8
2x+y≤8
x∈N+，y∈N+
，目标函数z=3x+y，某学生求得x=
8
3
，y=
8
3
时，zmax=
32
3
，这显然不合要求，正确答案应为x=______；y=______；zmax=______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网