题目内容
1.已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其左右焦点分别为F1,F2,焦距为4,双曲线C2:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1,C1,C2的离心率互为倒数.(1)求椭圆的标准方程;
(2)过F2作直线交抛物线y2=2x于A,B两点,射线OA,OB分别交椭圆C1于点D,E.证明:$\frac{|OD||OE|}{|DE|}$为定值.
分析 (1)由双曲线C2:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1,可得离心率e2=$\sqrt{1+\frac{2}{4}}$=$\frac{\sqrt{6}}{2}$.于是椭圆的离心率$\frac{c}{a}$=$\frac{2}{\sqrt{6}}$=$\frac{\sqrt{6}}{3}$,又2c=4,a2=b2+c2,联立解出即可.
(2)设直线AB的方程为:my=x-2,A(x1,y1),B(x2,y2).与抛物线方程联立化为y2-2my-4=0,利用根与系数的关系与斜率计算公式可得:kOA•kOB=$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-1.因此OA⊥OB.设直线OA的方程为:y=kx,则直线OB的方程为:y=-$\frac{1}{k}$x.分别与椭圆方程联立解得D,E的坐标,利用两点之间的距离公式及其勾股定理可得|OD|2,|OE|2.|DE|2=|OD|2+|OE|2,即可证明$\frac{|OD{|}^{2}|OE{|}^{2}}{|DE{|}^{2}}$=$\frac{3}{2}$.
解答 (1)解:由双曲线C2:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1,可得离心率e2=$\sqrt{1+\frac{2}{4}}$=$\frac{\sqrt{6}}{2}$.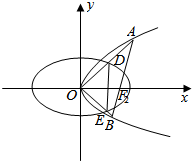
∴椭圆的离心率$\frac{c}{a}$=$\frac{2}{\sqrt{6}}$=$\frac{\sqrt{6}}{3}$,
又2c=4,a2=b2+c2,
解得c=2,a=$\sqrt{6}$,b=$\sqrt{2}$.
∴椭圆的标准方程是$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}$=1.
(2)证明:设直线AB的方程为:my=x-2,A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{my=x-2}\\{{y}^{2}=2x}\end{array}\right.$,化为y2-2my-4=0,
∴y1+y2=2m,y1y2=-4.
∴kOA•kOB=$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=$\frac{{y}_{1}{y}_{2}}{(m{y}_{1}+2)(m{y}_{2}+2)}$=$\frac{{y}_{1}{y}_{2}}{{m}^{2}{y}_{1}{y}_{2}+2m({y}_{1}+{y}_{2})+4}$=$\frac{-4}{-4{m}^{2}+4{m}^{2}+4}$=-1.
∴OA⊥OB.
设直线OA的方程为:y=kx,则直线OB的方程为:y=-$\frac{1}{k}$x.
联立$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}+3{y}^{2}=6}\end{array}\right.$,解得${x}_{D}^{2}$=$\frac{6}{1+3{k}^{2}}$,${y}_{D}^{2}$=$\frac{6{k}^{2}}{1+3{k}^{2}}$,∴|OD|2=$\frac{6(1+{k}^{2})}{1+3{k}^{2}}$.
同理可得:${x}_{E}^{2}$=$\frac{6{k}^{2}}{3+{k}^{2}}$,${y}_{E}^{2}$=$\frac{6}{3+{k}^{2}}$,∴|OE|2=$\frac{6(1+{k}^{2})}{3+{k}^{2}}$.
∴|DE|2=|OD|2+|OE|2=$\frac{6(1+{k}^{2})}{1+3{k}^{2}}$+$\frac{6(1+{k}^{2})}{3+{k}^{2}}$.
∴$\frac{|OD{|}^{2}|OE{|}^{2}}{|DE{|}^{2}}$=$\frac{6(1+{k}^{2})}{4(1+{k}^{2})}$=$\frac{3}{2}$.
∴$\frac{|OD||OE|}{|DE|}$为定值$\frac{\sqrt{6}}{2}$.
点评 本题考查了圆锥曲线的标准方程及其性质、直线与椭圆及其抛物线相交问题转化为一元二次方程的根与系数的关系、两点之间的距离公式、勾股定理、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于难题.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案| A. | y=x-2-2 | B. | y=x-2+2 | C. | y=(x-2)-2 | D. | y=(x+2)-2 |
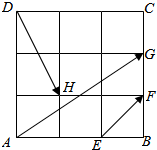 在如图所示的图形中,每个小四边形都是边长相等的正方形,则向量$\overrightarrow{AG}$=( )
在如图所示的图形中,每个小四边形都是边长相等的正方形,则向量$\overrightarrow{AG}$=( )| A. | $\frac{2}{3}\overrightarrow{EF}+\frac{7}{3}\overrightarrow{DH}$ | B. | $\frac{5}{3}\overrightarrow{EF}+\frac{4}{3}\overrightarrow{DH}$ | C. | $\frac{8}{3}\overrightarrow{EF}+\frac{1}{3}\overrightarrow{DH}$ | D. | $\frac{10}{3}\overrightarrow{EF}-\frac{1}{3}\overrightarrow{DH}$ |