题目内容
(本小题满分14分)(注意:在试题卷上作答无效)
已知曲线 ,从
,从 上的点
上的点 作
作 轴的垂线,交
轴的垂线,交 于点
于点 ,再从点
,再从点 作
作 轴的垂线,交
轴的垂线,交 于点
于点 ,设
,设

(1)求数列 的通项公式;
的通项公式;
(2)记 ,数列
,数列 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小
的大小 ;
;
(3)记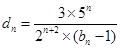 ,数列
,数列 的前
的前 项和为
项和为 ,试证明:
,试证明: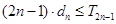

【答案】
(1)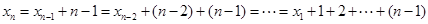
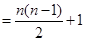 ;
;
(2)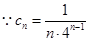 ,由
,由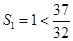 ,
,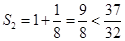 ,
,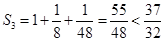 ,
,
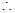 当
当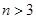 时,
时,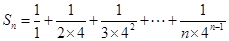
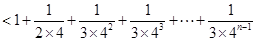
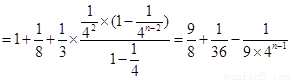
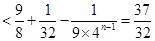 ;
;
(3)见解析。
【解析】(1) 依题意确定点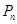 的坐标为
的坐标为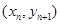 ,从而可得
,从而可得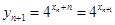 ,
,
所以可得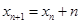 ,所以再采用累加的方法求出
,所以再采用累加的方法求出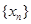 通项即可.
通项即可.
(2)先求出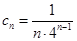 ,然后先求出S1,S2,S3验证均满足小于
,然后先求出S1,S2,S3验证均满足小于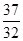 ,
,
然后证明当n>3时,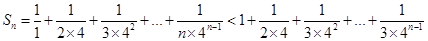 ,采用了不等式放缩后易证.n>3时,
,采用了不等式放缩后易证.n>3时,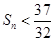 .
.
(3)先确定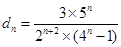 ,可得
,可得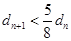 ,
,
然后可以利用此不等式进行放缩,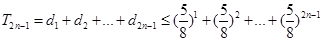 这是解决此题的突破口.
这是解决此题的突破口.
(1)依题意点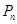 的坐标为
的坐标为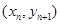 ,
,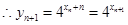 ,
,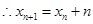 ,
,
......2分
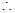
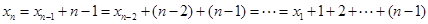
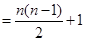 ;
;
......4分
(2)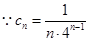 ,由
,由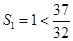 ,
,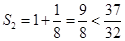 ,
,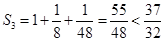 ,
,
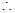 当
当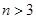 时,
时,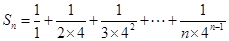
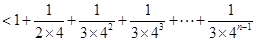
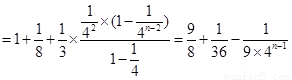
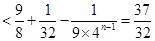 ;......8分
;......8分
(3)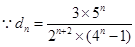 ,所以易证:
,所以易证: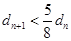 ,
,
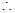 当
当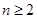 时,
时,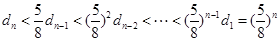 ,
,
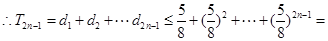
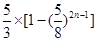 ,(当
,(当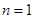 时取“
时取“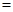 ”)......11分
”)......11分
另一方面,当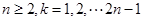 时,有:
时,有:

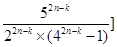
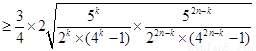
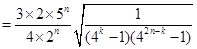
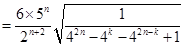 ,
,
又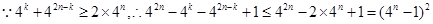 ,
,
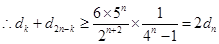 ,
,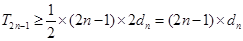 .所以
.所以
对任意的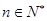 ,都有
,都有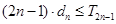
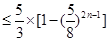 .......14分
.......14分

练习册系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)