题目内容
已知函数f(x)=sinωx(ω>0)在区间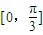 上单调递增,在区间
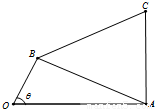
上单调递增,在区间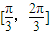 上单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足
上单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足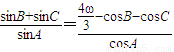 .
.(Ⅰ)证明:b+c=2a;
(Ⅱ)若b=c,设∠AOB=θ,(0<θ<π),OA=2OB=2,求四边形OACB面积的最大值.
【答案】分析:(Ⅰ)由题意知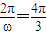 ,解之可得ω,代入已知条件化简可得sinC+sinB=2sinA,再由正弦定理可得b+c=2a;
,解之可得ω,代入已知条件化简可得sinC+sinB=2sinA,再由正弦定理可得b+c=2a;
(Ⅱ)由条件和(Ⅰ)的结论可得△ABC为等边三角形,可得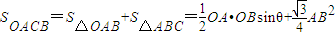 ,可化简为
,可化简为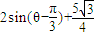 ,由θ的范围可得结论.
,由θ的范围可得结论.
解答:解:(Ⅰ)由题意知: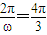 ,解得
,解得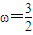 …(2分)
…(2分)
∵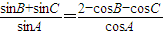 ,
,
∴sinBcosA+sinCcosA=2sinA-cosBsinA-cosCsinA,
∴sinBcosA+cosBsinA+sinCcosA+cosCsinA=2sinA,
∴sin(A+B)+sin(A+C)=2sinA…(4分)
∴sinC+sinB=2sinA,
∴b+c=2a…(6分)
(Ⅱ)因为b+c=2a,b=c,所以a=b=c,所以△ABC为等边三角形,
∴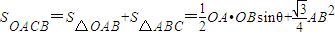 …(8分)
…(8分)
=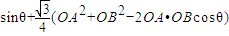 …(9分)
…(9分)
=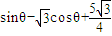 =
=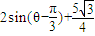 ,…(10分)
,…(10分)
∵θ∈(0,π),∴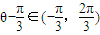 ,
,
当且仅当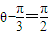 ,即
,即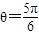 时取最大值,SOACB的最大值为
时取最大值,SOACB的最大值为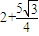 …(12分)
…(12分)
点评:本题考查两角和与差的三角函数公式,涉及余弦定理和三角形的面积,属中档题.
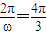 ,解之可得ω,代入已知条件化简可得sinC+sinB=2sinA,再由正弦定理可得b+c=2a;
,解之可得ω,代入已知条件化简可得sinC+sinB=2sinA,再由正弦定理可得b+c=2a;(Ⅱ)由条件和(Ⅰ)的结论可得△ABC为等边三角形,可得
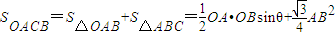 ,可化简为
,可化简为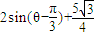 ,由θ的范围可得结论.
,由θ的范围可得结论.解答:解:(Ⅰ)由题意知:
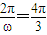 ,解得
,解得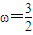 …(2分)
…(2分)∵
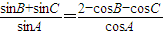 ,
,∴sinBcosA+sinCcosA=2sinA-cosBsinA-cosCsinA,
∴sinBcosA+cosBsinA+sinCcosA+cosCsinA=2sinA,
∴sin(A+B)+sin(A+C)=2sinA…(4分)
∴sinC+sinB=2sinA,
∴b+c=2a…(6分)
(Ⅱ)因为b+c=2a,b=c,所以a=b=c,所以△ABC为等边三角形,
∴
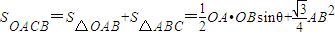 …(8分)
…(8分)=
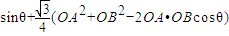 …(9分)
…(9分)=
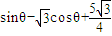 =
=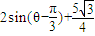 ,…(10分)
,…(10分)∵θ∈(0,π),∴
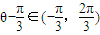 ,
,当且仅当
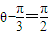 ,即
,即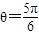 时取最大值,SOACB的最大值为
时取最大值,SOACB的最大值为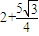 …(12分)
…(12分)点评:本题考查两角和与差的三角函数公式,涉及余弦定理和三角形的面积,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
