题目内容
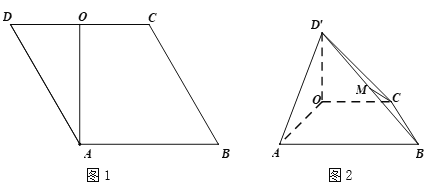
【题目】在菱形![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 的中点(如图1).将
的中点(如图1).将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 的中点(如图2).
的中点(如图2).
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)当四棱锥![]() 的体积为
的体积为![]() 时,求
时,求![]() 的值.
的值.
【答案】(Ⅰ)见解析. (Ⅱ)见解析. (Ⅲ) ![]() .
.
【解析】
(Ⅰ)证明OD'⊥AO. 推出OD'⊥平面ABCO. 然后证明OD'⊥BC.(Ⅱ)取P为线段AD'的中点,连接OP,PM;证明四边形OCMP为平行四边形,然后证明CM∥平面AOD';(Ⅲ)说明OD'是四棱锥D'﹣ABCO的高.通过体积公式求解即可.
(Ⅰ)证明:因为在菱形![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,
所以![]() .
.
因为平面![]() 平面
平面![]()
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() .
.
(Ⅱ)证明:如图,取![]() 为线段
为线段![]() 的中点,连接OP,PM;
的中点,连接OP,PM;
因为在![]() 中,
中,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,
的中点,
所以![]() ,
,![]() .
.
因为![]() 是线段
是线段![]() 的中点,菱形
的中点,菱形![]() 中,
中,![]() ,
,![]() ,
,
所以![]() .
.
所以![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
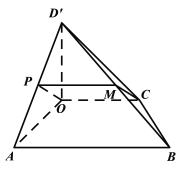
(Ⅲ)由(Ⅰ)知![]() 平面
平面![]() .
.
所以![]() 是四棱锥
是四棱锥![]() 的高,又S=
的高,又S=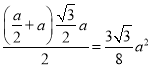 ,
,![]()
因为![]() ,
,
所以![]() .
.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目