题目内容
【题目】
设函数f(x)=alnx﹣bx2(x>0).
(1)若函数f(x)在x=1处于直线![]() 相切,求函数f(x)在
相切,求函数f(x)在![]() 上的最大值;
上的最大值;
(2)当b=0时,若不等式f(x)≥m+x对所有的a∈[1,![]() ],x∈[1,e2]都成立,求实数m的取值范围.
],x∈[1,e2]都成立,求实数m的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)(﹣∞,2﹣e2].
;(Ⅱ)(﹣∞,2﹣e2].
【解析】试题分析:(1)对函数求导,利用函数在![]() 处与
处与![]() 相切,可得关于
相切,可得关于![]() 方程,求出
方程,求出![]() ,再利用导函数判断函数在
,再利用导函数判断函数在![]() 上的单调性,结合单调性求得函数最大值.(Ⅱ)用分离变量法,将原问题转化为
上的单调性,结合单调性求得函数最大值.(Ⅱ)用分离变量法,将原问题转化为![]() ,对所有的
,对所有的![]() ,构造函数
,构造函数![]() 利用一次函数单调性,求出最小值
利用一次函数单调性,求出最小值![]() ,再进一步利用函数单调性,求出最小值后可得
,再进一步利用函数单调性,求出最小值后可得![]() 的范围.
的范围.
试题解析:(Ⅰ)∵f′(x)=![]() ﹣2bx,
﹣2bx,
又函数f(x)在x=1处与直线y=﹣![]() 相切,
相切,
∴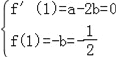 ,解得
,解得![]() .
.
f(x)=lnx﹣![]() x2,f′(x)=
x2,f′(x)=![]() ﹣x=﹣
﹣x=﹣![]() ,
,
当x∈[![]() ,1),f′(x)<0,f(x)递增,
,1),f′(x)<0,f(x)递增,
当x∈(1,e],f′(x)>0,f(x)递减.
即有f(x)的最大值为f(1)=﹣![]() ;
;
(Ⅱ)当b=0时,f(x)=alnx,
若不等式f(x)≥m+x对所有的a∈[1,![]() ],x∈[1,e2]都成立,
],x∈[1,e2]都成立,
即m≤alnx﹣x对所有的a∈[1,![]() ],x∈[1,e2]都成立,
],x∈[1,e2]都成立,
令h(a)=alnx﹣x,则h(a)为一次函数,
∴m≤h(a)min.
∵x∈[1,e2],∴lnx≥0,
∴h(a)在[1,![]() ]上单调递增,
]上单调递增,
∴h(a)min=h(1)=lnx﹣x,
∴m≤lnx﹣x对所有的x∈(1,e2]都成立.
由y=lnx﹣x(1<x≤e2)的导数为y′=![]() ﹣1<0,
﹣1<0,
则函数y=lnx﹣x(1<x≤e2)递减,
∵1<x≤e2,∴lnx﹣x≥2﹣e2,
则m≤2﹣e2.
则实数m的取值范围为(﹣∞,2﹣e2]

 名校课堂系列答案
名校课堂系列答案【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩进行统计. 请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
分组 | 频数 | 频率 |
50.5~60.5 | 6 | 0.08 |
60.5~70.5 | 0.16 | |
70.5~80.5 | 15 | |
80.5~90.5 | 24 | 0.32 |
90.5~100.5 | ||
合计 | 75 | 1.00 |
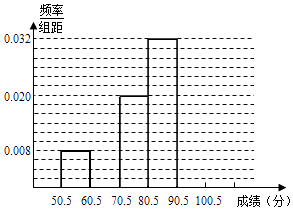
(1)填充频率分布表的空格;
(2)补全频率分布直方图;
(3)根据频率分布直方图求此次“环保知识竞赛”的平均分为多少?

