题目内容
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,两焦点与短轴的一个端点的连线构成的三角形面积为
,两焦点与短轴的一个端点的连线构成的三角形面积为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)设与圆![]() 相切的直线
相切的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点(
两点(![]() 为坐标原点),
为坐标原点),![]() 的最大值.
的最大值.
【答案】I.![]() ;Ⅱ.2
;Ⅱ.2
【解析】
I:根据离心率得到![]() ,由三角形面积公式得到
,由三角形面积公式得到![]() ,进而求出参数值,和方程;Ⅱ:当AB
,进而求出参数值,和方程;Ⅱ:当AB![]() x轴时,
x轴时,![]() ,当AB与x轴不垂直时,设直线AB的方程为
,当AB与x轴不垂直时,设直线AB的方程为![]() ,根据直线和圆的位置关系得到
,根据直线和圆的位置关系得到![]() ,由
,由![]() =
=![]() ,借助于韦达定理表示求解即可.
,借助于韦达定理表示求解即可.
I.由题设:![]()
两焦点与短轴的一个端点的连线构成的三角形面积为![]() ,
,
解得![]()
∴椭圆C的方程为![]()
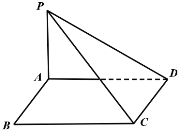
Ⅱ.设![]()
1.当AB![]() x轴时,
x轴时,![]()
2.当AB与x轴不垂直时,设直线AB的方程为![]()
由已知![]() ,得
,得![]()
设三角形OAB的高为h即圆的半径,直线和圆的切点为M点,根据几何关系得到:![]() =
=![]() ,
,
把![]() 代入椭圆方程消去y,
代入椭圆方程消去y,
整理得![]() ,
,
有![]()
得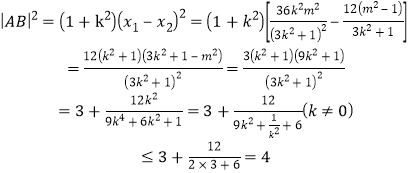
当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
当![]() 时,
时,![]()
综上所述![]()

【题目】空气质量按照空气质量指数大小分为七档(五级),相对应空气质量的七个类别,指数越大,说明污染的情况越严重,对人体危害越大.
指数 | 级别 | 类别 | 户外活动建议 |
| Ⅰ | 优 | 可正常活动 |
| Ⅱ | 良 | |
| Ⅲ | 轻微污染 | 易感人群症状有轻度加剧,健康人群出现刺激症状,心脏病和呼吸系统疾病患者应减少体积消耗和户外活动. |
| 轻度污染 | ||
| Ⅳ | 中度污染 | 心脏病和肺病患者症状显著加剧,运动耐受力降低,健康人群中普遍出现症状,老年人和心脏病、肺病患者应减少体力活动. |
| 中度重污染 | ||
| Ⅴ | 重污染 | 健康人运动耐受力降低,由明显强烈症状,提前出现某些疾病,老年人和病人应当留在室内,避免体力消耗,一般人群应尽量减少户外活动. |
现统计邵阳市市区2016年1月至11月连续60天的空气质量指数,制成如图所示的频率分布直方图.
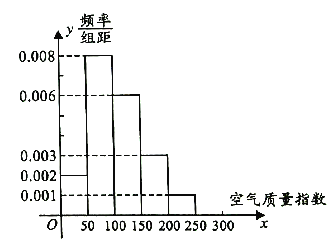
(1)求这60天中属轻度污染的天数;
(2)求这60天空气质量指数的平均值;
(3)一般地,当空气质量为轻度污染或轻度污染以上时才会出现雾霾天气,且此时出现雾霾天气的概率为![]() ,请根据统计数据,求在未来2天里,邵阳市恰有1天出现雾霾天气的概率.
,请根据统计数据,求在未来2天里,邵阳市恰有1天出现雾霾天气的概率.
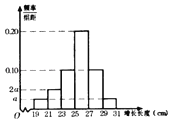
【题目】为了解某养殖产品在某段时间内的生长情况,在该批产品中随机抽取了120件样本,测量其增长长度(单位:![]() ),经统计其增长长度均在区间
),经统计其增长长度均在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成频率分布直方图,如图所示其中增长长度为
分成6组,制成频率分布直方图,如图所示其中增长长度为![]() 及以上的产品为优质产品.
及以上的产品为优质产品.
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)已知这120件产品来自于![]() ,
,![]() 两个试验区,部分数据如下列联表:
两个试验区,部分数据如下列联表:
|
| 合计 | |
优质产品 | 20 | ||
非优质产品 | 60 | ||
合计 |
将联表补充完整,并判断是否有![]() 的把握认为优质产品与
的把握认为优质产品与![]() ,
,![]() 两个试验区有关系,并说明理由;
两个试验区有关系,并说明理由;
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
(Ⅲ)以样本的频率代表产品的概率,从这批产品中随机抽取4件进行分析研究,计算抽取的这4件产品中含优质产品的件数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.