题目内容
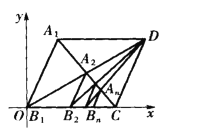
【题目】边长为1的菱形![]() 的两对角线交于
的两对角线交于![]() ,过
,过![]() 作A2B2∥A1B1交
作A2B2∥A1B1交![]() 于
于![]() 连结
连结![]() 交
交![]() 于
于![]() ,过
,过![]() 作A3B3∥A1B1交
作A3B3∥A1B1交![]() 于
于![]() ,…,这样作下去得
,…,这样作下去得![]() 以
以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系,设以
轴,建立平面直角坐标系,设以![]() 为半径,圆心在
为半径,圆心在![]() ,轴上的一列圆
,轴上的一列圆![]() 依次相外切(即
依次相外切(即![]() 与
与![]() 外切,
外切,![]() ),若圆T1与抛物线
),若圆T1与抛物线![]() 相切.求证:所有的圆
相切.求证:所有的圆![]() 都与抛物线
都与抛物线![]() 相切.
相切.
【答案】见解析
【解析】
如图,由题设知![]()
猜测:![]()
用数学归纳法证明
当![]() 时,显然成立.
时,显然成立.
假设![]() 时,有
时,有![]() .
.
由三角形相似有![]() 及
及![]()
此两式相加即证得![]() .
.
由归纳法原理,知![]() 时,
时, ![]()
设以![]() 为半径且圆心在y轴上的圆与
为半径且圆心在y轴上的圆与![]() 相切的圆心坐标为
相切的圆心坐标为![]() .则由
.则由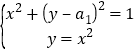 得
得![]() .
.
再由其![]() 求得
求得![]() ①
①
设以![]() 为半径的圆依次外切且圆心在y轴上时的圆心坐标为
为半径的圆依次外切且圆心在y轴上时的圆心坐标为![]() ,其中
,其中![]() .
.
则![]()
从而,![]()
即![]()
又![]()
故![]() ②
②
![]() . ③
. ③
再由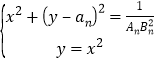
有![]() .
.
则由![]() ,再将③代入得
,再将③代入得![]() 这说明这些圆均与抛物线
这说明这些圆均与抛物线![]() 相切.
相切.

练习册系列答案
相关题目
