题目内容
已知集合A={a1,a2,a3,…,an},记和ai+aj(1≤i<j≤n)中所有不同值的个数为M(A).如当A={1,2,3,4}时,由1+2=3,1+3=4,1+4=2+3=5,2+4=6,3+4=7,得M(A)=5.对于集合B={b1,b2,b3,…,bn},若实数b1,b2,b3,…,bn成等差数列,则M(B)= .
2n-3
由题意可知,b1,b2,b3,…,bn成等差数列且各项不相同,由等差数列的性质,数列中任意两项之和,只要序号之和不同,该两项之和就不同,那么在从1到n中任意两项的序号之和最小的是3,然后是4,5,…且可以连续地取到,最大的和是n+(n-1)=2n-1,共有2n-3个不同的和.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
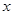 的二次方程
的二次方程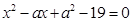 和
和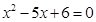 的解集分别是集合
的解集分别是集合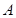 和
和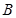 ,若
,若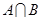 为单元素集,求
为单元素集,求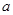 的值.
的值.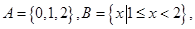 则
则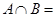 ( )
( )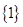
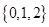
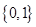
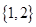
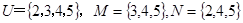 ,则( )
,则( )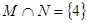
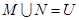
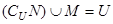
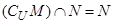
 ,
, ,则
,则 ( )
( )


