题目内容
如图,直线PA垂直于圆O所在的平面,
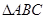 内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①
内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①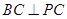 ;②
;②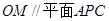 ;③点B到平面PAC的距离等于线段BC的长.其中真命题的个数为 ( )
;③点B到平面PAC的距离等于线段BC的长.其中真命题的个数为 ( )
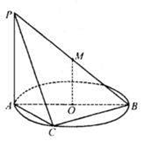

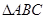 内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①
内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①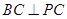 ;②
;②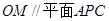 ;③点B到平面PAC的距离等于线段BC的长.其中真命题的个数为 ( )
;③点B到平面PAC的距离等于线段BC的长.其中真命题的个数为 ( )
| A.3 | B.2 | C.1 | D.0 |
A
分析:对于①,先根据线面垂直的判定定理证明BC⊥面PAC,然后根据线面垂直的判定定理得到结论;对于②,根据线面平行的判定定理进行判定即可;对于③,根据点到面的距离的定义进行判定即可.
解答:解:∵PA⊥圆O所在的平面,BC?圆O所在的平面∴PA⊥BC
而BC⊥AC,PA∩AC=A
∴BC⊥面PAC,而PC?面PAC
∴BC⊥PC,故①正确;
∵点M为线段PB的中点,点O为AB的中点
∴OM∥PA,而OM?面PAC,PA?面PAC
∴OM∥平面APC,故②正确;
∵BC⊥面PAC
∴点B到平面PAC的距离等于线段BC的长,故③正确
故选A
解答:解:∵PA⊥圆O所在的平面,BC?圆O所在的平面∴PA⊥BC
而BC⊥AC,PA∩AC=A
∴BC⊥面PAC,而PC?面PAC
∴BC⊥PC,故①正确;
∵点M为线段PB的中点,点O为AB的中点
∴OM∥PA,而OM?面PAC,PA?面PAC
∴OM∥平面APC,故②正确;
∵BC⊥面PAC
∴点B到平面PAC的距离等于线段BC的长,故③正确
故选A

练习册系列答案
相关题目
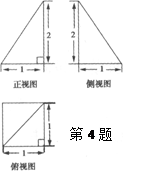
 cm3
cm3 cm3
cm3 cm3
cm3 cm3
cm3



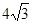
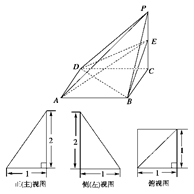
 4分)右图为一简单组合体,其底面
4分)右图为一简单组合体,其底面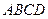 为正方形,
为正方形,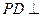 平面
平面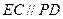 ,
,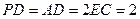
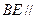 平面
平面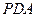
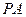 与平面
与平面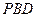 所成角的
所成角的 大小。
大小。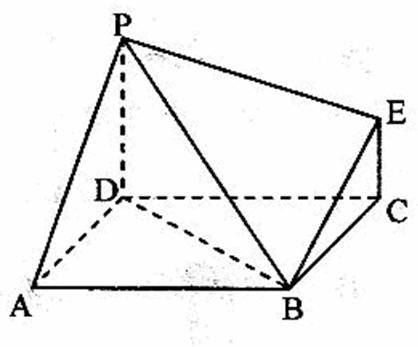



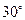 纬线的长度为
纬线的长度为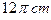 ,该地球仪的半径是__________cm,
,该地球仪的半径是__________cm,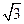 ,则其外接球的表面积是 ...
,则其外接球的表面积是 ...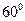 纬线长和赤道长的比值为
纬线长和赤道长的比值为