题目内容
|
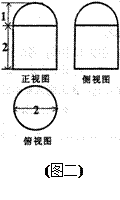
(理)如图是一个几何体的三视图,其中正视图和侧视图所对应的三角形是边长为2的正三角形,俯视图对应的四边形为正方形,则这个几何体的体积等于 ( ) 
|
C
考点:
分析:易得此几何体为四棱锥,利用相应的三角函数可得四棱锥的高,体积=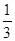 ×底面积×高,把相关数值代入即可求解.
×底面积×高,把相关数值代入即可求解.
解答:解:由主视图和左视图为等腰三角形可得此几何体为锥体,由俯视图为四边形可得此几何体为四棱锥,
∵主视图为边长为2的正三角形,
∴正三角形的高,也就是棱锥的高为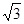 ,俯视图的边长为2,
,俯视图的边长为2,
∴四棱锥的体积=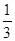 ×2×2×
×2×2×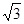 =
=
故选C.
点评:解决本题的关键是得到该几何体的形状,易错是确定四棱锥的底面边长与高的大小.
分析:易得此几何体为四棱锥,利用相应的三角函数可得四棱锥的高,体积=
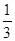 ×底面积×高,把相关数值代入即可求解.
×底面积×高,把相关数值代入即可求解.解答:解:由主视图和左视图为等腰三角形可得此几何体为锥体,由俯视图为四边形可得此几何体为四棱锥,
∵主视图为边长为2的正三角形,
∴正三角形的高,也就是棱锥的高为
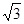 ,俯视图的边长为2,
,俯视图的边长为2,∴四棱锥的体积=
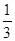 ×2×2×
×2×2×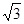 =
=
故选C.
点评:解决本题的关键是得到该几何体的形状,易错是确定四棱锥的底面边长与高的大小.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目


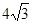








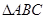 内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①
内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①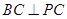 ;②
;②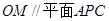 ;③点B到平面PAC的距离等于线段BC的长.其中真命题的个数为 ( )
;③点B到平面PAC的距离等于线段BC的长.其中真命题的个数为 ( )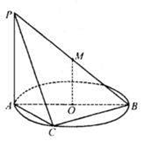
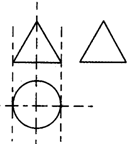
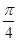
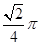
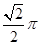
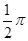
 轴的平行四边形,采用斜二测画法做出其直观图,其直观图面积是原图形面积的
轴的平行四边形,采用斜二测画法做出其直观图,其直观图面积是原图形面积的 倍
倍 倍
倍 倍
倍