题目内容
过双曲线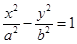 的左焦点F作⊙O:
的左焦点F作⊙O: 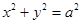 的两条切线,记切点为A,B,双曲线左顶点为C,若
的两条切线,记切点为A,B,双曲线左顶点为C,若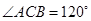 ,则双曲线的离心率为____________.
,则双曲线的离心率为____________.
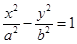 的左焦点F作⊙O:
的左焦点F作⊙O: 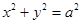 的两条切线,记切点为A,B,双曲线左顶点为C,若
的两条切线,记切点为A,B,双曲线左顶点为C,若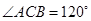 ,则双曲线的离心率为____________.
,则双曲线的离心率为____________.2
试题分析:因为∠ACB=120°,OA=OC,所以∠AOC=60°。
∵FA是圆的切线,∴∠AFO=30°,∴OF=2OC,∴c=2a,∴e=2
故答案为2。
点评:中档题,解题的关键是熟练明确双曲线与圆的位置关系,结合有关条件确定a,b,c的关系。

练习册系列答案
相关题目
 的左、右焦点分别是
的左、右焦点分别是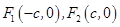 ,Q是椭圆外的动点,满足
,Q是椭圆外的动点,满足 .点
.点 是线段
是线段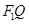 与该椭圆的交点,点T是
与该椭圆的交点,点T是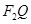 的中点.
的中点.
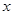 为点
为点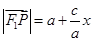 ;
;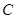 的方程.
的方程.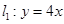 ,
,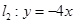 ,过
,过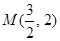 的直线
的直线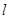 与
与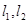 分别交于
分别交于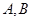 ,若
,若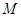 是线段
是线段 的中点,则
的中点,则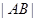 等于( )
等于( )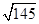
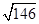
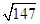
 ( )
( )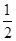
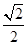
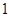
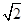
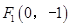 、
、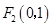 且过点
且过点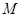
 椭圆;
椭圆; 有相同的渐近线,且过点
有相同的渐近线,且过点 的双曲线.
的双曲线.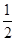 ,短轴长为4
,短轴长为4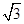 .
.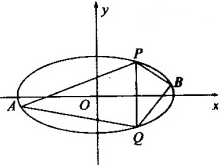
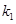 ,直线PB的斜率为
,直线PB的斜率为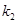 ,判断
,判断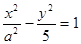 的右焦点为(3,0),则该双曲线的离心率等于 ( )
的右焦点为(3,0),则该双曲线的离心率等于 ( )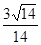

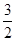 .
.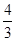
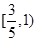


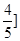
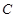 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,其左、右焦点分别为
轴上,其左、右焦点分别为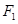 、
、 ,短轴长为
,短轴长为 ,点
,点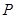 在椭圆
在椭圆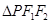 的周长为6.
的周长为6. 的直线与椭圆相交于A、B两点,试问在x轴上是否存在一个定点M使
的直线与椭圆相交于A、B两点,试问在x轴上是否存在一个定点M使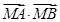 恒为定值?若存在求出该定值及点M的坐标,若不存在请说明理由.
恒为定值?若存在求出该定值及点M的坐标,若不存在请说明理由.