题目内容
等比数列{cn}满足cn+1+cn=5•22n-1,n∈N*,数列{an}满足an=log2cn
(Ⅰ)求{an}的通项公式;
(Ⅱ)数列{bn}满足bn=
,Tn为数列{bn}的前n项和.求证:Tn<
;
(Ⅲ)是否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列?若存在,求出所有m,n 的值;若不存在,请说明理由.
(Ⅰ)求{an}的通项公式;
(Ⅱ)数列{bn}满足bn=
| 1 |
| an•an+1 |
| 1 |
| 2 |
(Ⅲ)是否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列?若存在,求出所有m,n 的值;若不存在,请说明理由.
分析:(Ⅰ)先根据cn+1+cn=5•22n-1求出公比q和首项,从而求出数列{cn}的通项公式,即可求得{an}的通项公式;
(Ⅱ)根据数列通项的特点可利用裂项求和法求出数列{bn}的前n项和Tn,从而可证得Tn<
;
(Ⅲ)假设存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列,建立等式关系,用m表示出n,再根据m∈N*,m>1,可求出所求.
(Ⅱ)根据数列通项的特点可利用裂项求和法求出数列{bn}的前n项和Tn,从而可证得Tn<
| 1 |
| 2 |
(Ⅲ)假设存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列,建立等式关系,用m表示出n,再根据m∈N*,m>1,可求出所求.
解答:解(Ⅰ)∵cn+1+cn=5•22n-1,n∈N+,
∴c1+c2=10,c2+c3=q(c1+c2)=40,
∴公比q=4,
∵c1+c2=c1+c1q=10,
解得c1=2,
∴{cn}的通项公式为cn=2•4n-1=22n-1,
∴an=log2cn=2n-1;
(Ⅱ)∵bn=
=
(
-
),
∴Tn=
[(1-
)+(
-
)+…+(
-
)]=
(1-
),
∵n∈N*,
∴
>0,∴Tn<
;
(Ⅲ)假设存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列,
则(
)2=
•
,
∴
=
>0,
∵分子为正,
∴1-
<m<1+
,
∵m∈N*,m>1,
∴m=2,n=12,
当且仅当m=2,n=12时,T1,Tm,Tn成等比数列.
∴c1+c2=10,c2+c3=q(c1+c2)=40,
∴公比q=4,
∵c1+c2=c1+c1q=10,
解得c1=2,
∴{cn}的通项公式为cn=2•4n-1=22n-1,
∴an=log2cn=2n-1;
(Ⅱ)∵bn=
| 1 |
| an•an+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
∵n∈N*,
∴
| 1 |
| 2n+1 |
| 1 |
| 2 |
(Ⅲ)假设存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列,
则(
| m |
| 2m+1 |
| 1 |
| 3 |
| n |
| 2n+1 |
∴
| 3 |
| n |
| -2m2+4m+1 |
| m2 |
∵分子为正,
∴1-
| ||
| 2 |
| ||
| 2 |
∵m∈N*,m>1,
∴m=2,n=12,
当且仅当m=2,n=12时,T1,Tm,Tn成等比数列.
点评:本题主要考查了数列的递推关系,等比关系的确定以及裂项求和法的应用,同时考查了分析问题与解决问题的能力,属于中档题.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
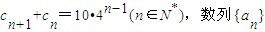 的前n项和为Sn,且an=log2cn.
的前n项和为Sn,且an=log2cn.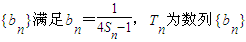 的前n项和,是否存在正整数m,(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由.
的前n项和,是否存在正整数m,(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由.