题目内容
等比数列{cn}满足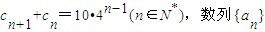 的前n项和为Sn,且an=log2cn.
的前n项和为Sn,且an=log2cn.(I)求an,Sn;
(II)数列
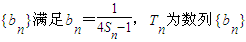 的前n项和,是否存在正整数m,(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由.
的前n项和,是否存在正整数m,(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由.
【答案】分析:(Ⅰ)由已知结合等比数列的性质可求q=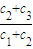 ,然后利用已知递推公式,令n=1可求c1,从而可求cn,进而可求an,由等差数列的求和公式可求sn
,然后利用已知递推公式,令n=1可求c1,从而可求cn,进而可求an,由等差数列的求和公式可求sn
(Ⅱ)由(Ⅰ)知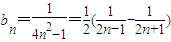 ,利用裂项求和可求Tn,然后假设存在正整数m(m>1)满足题意,则由等比数列的 性质可建立关于m的方程,求解即可
,利用裂项求和可求Tn,然后假设存在正整数m(m>1)满足题意,则由等比数列的 性质可建立关于m的方程,求解即可
解答:解:(Ⅰ)c1+c2=10,c2+c3=40,
所以公比q=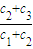 =4…(2分)
=4…(2分)
由c2+c1=c1+4c1=10得c1=2
所以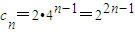 …(4分)
…(4分)
所以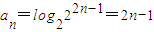 …(5分)
…(5分)
由等差数列的求和公式可得,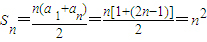 …(6分)
…(6分)
(Ⅱ)由(Ⅰ)知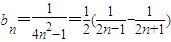
于是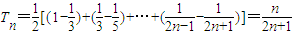 …(8分)
…(8分)
假设存在正整数m(m>1),使得T1,Tm,T6m成等比数列,
则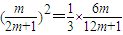 ,…(10分)
,…(10分)
整理得4m2-7m-2=0,
解得 或 m=2
或 m=2
由m∈N*,m>1,得m=2,
因此,存在正整数m=2,使得T1,Tm,T6m成等比数列 …(12分)
点评:本题主要考查了等比数列的性质及通项公式的求解,等差数列的求和公式及数列的裂项求和方法的应用.
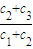 ,然后利用已知递推公式,令n=1可求c1,从而可求cn,进而可求an,由等差数列的求和公式可求sn
,然后利用已知递推公式,令n=1可求c1,从而可求cn,进而可求an,由等差数列的求和公式可求sn(Ⅱ)由(Ⅰ)知
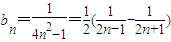 ,利用裂项求和可求Tn,然后假设存在正整数m(m>1)满足题意,则由等比数列的 性质可建立关于m的方程,求解即可
,利用裂项求和可求Tn,然后假设存在正整数m(m>1)满足题意,则由等比数列的 性质可建立关于m的方程,求解即可解答:解:(Ⅰ)c1+c2=10,c2+c3=40,
所以公比q=
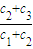 =4…(2分)
=4…(2分)由c2+c1=c1+4c1=10得c1=2
所以
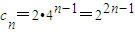 …(4分)
…(4分)所以
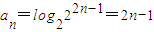 …(5分)
…(5分)由等差数列的求和公式可得,
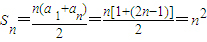 …(6分)
…(6分)(Ⅱ)由(Ⅰ)知
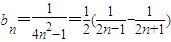
于是
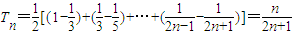 …(8分)
…(8分)假设存在正整数m(m>1),使得T1,Tm,T6m成等比数列,
则
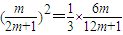 ,…(10分)
,…(10分)整理得4m2-7m-2=0,
解得
 或 m=2
或 m=2由m∈N*,m>1,得m=2,
因此,存在正整数m=2,使得T1,Tm,T6m成等比数列 …(12分)
点评:本题主要考查了等比数列的性质及通项公式的求解,等差数列的求和公式及数列的裂项求和方法的应用.

练习册系列答案
相关题目