题目内容
(2013•淄博二模)等比数列{cn}满足cn+1+cn=10•4n-1(n∈N*),数列{an}的前n项和为Sn,且an=log2cn.
(I)求an,Sn;
(II)数列{bn}满足bn=
,Tn为数列{bn}的前n项和,是否存在正整数m,k(1<m<k),使得T1,Tm,Tk成等比数列?若存在,求出所有m,k的值;若不存在,请说明理由.
(I)求an,Sn;
(II)数列{bn}满足bn=
| 1 | 4Sn-1 |
分析:(Ⅰ)由已知令n=1,n=2可求,c1+c2,c2+c3,从而可求公比q,及c1,结合等比数列的通项公式可求cn,进而可求an,结合等差数列的求和公式可求sn
(Ⅱ)由(Ⅰ)知bn=
=
(
-
),利用裂项可求Tn,然后结合等比数列的性质可求满足条件的m,k
(Ⅱ)由(Ⅰ)知bn=
| 1 |
| 4n2-1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:解:(Ⅰ)由已知令n=1,n=2可得,c1+c2=10,c2+c3=40,所以公比q=4…(2分)
∴c1+c2=c1+4c1=10得c1=2
∴cn=2•4n-1=22n-1…(4分)
所以an=log222n-1=2n-1…(5分)
由等差数列的求和公式可得,Sn=
=
=n2…(6分)
(Ⅱ)由(Ⅰ)知bn=
=
(
-
)
于是Tn=
[(1-
)+(
-
)+…+(
-
)]=
…(9分)
假设存在正整数m,k(1<m<k),使得T1,Tm,Tk成等比数列,则(
)2=
×
,
可得
=
>0,所以-2m2+4m+1>0
从而有,1-
<m<1+
,
由m∈N*,m>1,得m=2…(11分)
此时k=12.
当且仅当m=2,k=12时,T1,Tm,Tk成等比数列.…(12分)
∴c1+c2=c1+4c1=10得c1=2
∴cn=2•4n-1=22n-1…(4分)
所以an=log222n-1=2n-1…(5分)
由等差数列的求和公式可得,Sn=
| n(a 1+an) |
| 2 |
| n[1+(2n-1)] |
| 2 |
(Ⅱ)由(Ⅰ)知bn=
| 1 |
| 4n2-1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
于是Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
假设存在正整数m,k(1<m<k),使得T1,Tm,Tk成等比数列,则(
| m |
| 2m+1 |
| 1 |
| 3 |
| k |
| 2k+1 |
可得
| 3 |
| k |
| -2m2+4m+1 |
| m2 |
从而有,1-
| ||
| 2 |
| ||
| 2 |
由m∈N*,m>1,得m=2…(11分)
此时k=12.
当且仅当m=2,k=12时,T1,Tm,Tk成等比数列.…(12分)
点评:本题主要考查了等比数列的性质及等比数列的通项公式的简单应用,数列的裂项求和方法的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
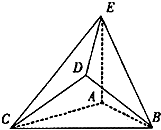 (2013•淄博二模)在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
(2013•淄博二模)在如图所示的几何体中,△ABC是边长为2的正三角形,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD. (2013•淄博二模)如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=
(2013•淄博二模)如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且AM=