题目内容
（Ⅰ）画出函数f（x）=x2-2x-3，x∈（-1，4]的图象；（Ⅱ）讨论当k为何实数值时，方程f（x）-k=0在（-1，4]上的解集为空集、单元素集、两元素集？
分析：（Ⅰ）根据二次函数的图象和性质，作出函数f（x）=x2-2x-3，x∈（-1，4]的图象；
（Ⅱ）求出函数f（x）在（-1，4]的值域根据函数的值域确定k的取值范围．
（Ⅱ）求出函数f（x）在（-1，4]的值域根据函数的值域确定k的取值范围．
解答：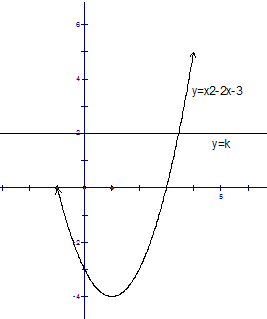
解：（I）f（x）=x2-2x-3=（x-1）2-4，则图象如右图所示，其中不含点（-1，0），含点（4，5）．
（II）原方程的解与两个函数y=x2-2x-3，x∈（-1，4]和y=k的图象的交点构成一一对应．
易用图象关系进行观察．
（1）当k＜-4或k＞5时，原方程在（-1，4]上的解集为空集；
（2）当k=-4或0≤k≤5时，原方程在（-1，4]上的解集为单元素集；
（3）当-4＜k＜0时，原方程在（-1，4]上的解集为两元素集．
解：（I）f（x）=x2-2x-3=（x-1）2-4，则图象如右图所示，其中不含点（-1，0），含点（4，5）．（II）原方程的解与两个函数y=x2-2x-3，x∈（-1，4]和y=k的图象的交点构成一一对应．
易用图象关系进行观察．
（1）当k＜-4或k＞5时，原方程在（-1，4]上的解集为空集；
（2）当k=-4或0≤k≤5时，原方程在（-1，4]上的解集为单元素集；
（3）当-4＜k＜0时，原方程在（-1，4]上的解集为两元素集．
点评：本题主要考查二次函数的图象和性质，根据配方即可得到函数的图象和性质．
练习册系列答案
华东师大版一课一练系列答案
相关题目
已知函数f（x）=sin2x+cos2x．
设f（x）为定义在R上的偶函数，当0≤x≤2时，y=x；当x＞2时，y=f（x）的图象是顶点为P（3，4）且过点A（2，2）的抛物线的一部分．
已知f（x）=