题目内容
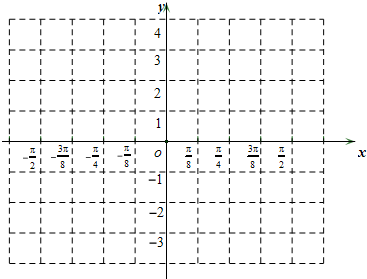 已知函数f(x)=sin2x+cos2x.
已知函数f(x)=sin2x+cos2x.(Ⅰ)当x∈(0,
| 11π |
| 24 |
(Ⅱ)画出函数f(x)在[0,
| π |
| 2 |
分析:(Ⅰ)f(x)=sin2x+cos2x=
sin(2x-
),再求x∈(0,
)时函数的取值范围.
(Ⅱ)由作图规则,先列表,再作图
| 2 |
| π |
| 4 |
| 11π |
| 24 |
(Ⅱ)由作图规则,先列表,再作图
解答:解:(Ⅰ)由题设f(x)=
sin(2x-
),当x∈(0,
π)时,2x-
∈(-
,
π);
∴sin(2x-
)∈(-
,1],故f(x)∈(-1,
];
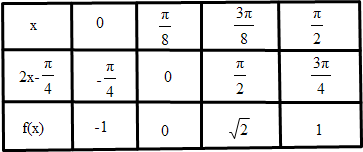
(Ⅱ)列表
图象如图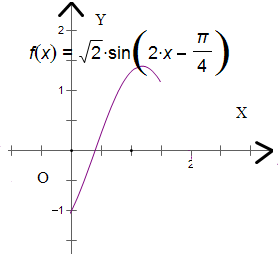
| 2 |
| π |
| 4 |
| 11 |
| 24 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| 3 |
∴sin(2x-
| π |
| 4 |
| ||
| 2 |
| 2 |
(Ⅱ)列表

图象如图
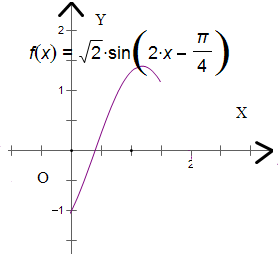
点评:本题考查正弦函数的定义域及值域,以及函数的图象作法,五点法作图,求解本题关键是将函数的解析式化简,再由函数的性质求值域,要掌握好五点法作图的步骤,

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
