题目内容
定义:设函数y=f(x)在(a,b)内可导,f'(x)为f(x)的导数,f''(x)为f'(x)的导数即f(x)的二阶导数,若函数y=f(x) 在(a,b)内的二阶导数恒大于等于0,则称函数y=f(x)是(a,b)内的下凸函数(有时亦称为凹函数).已知函数f(x)=xlnx
(1)证明函数f(x)=xlnx是定义域内的下凸函数,并在所给直角坐标系中画出函数f(x)=xlnx的图象;
(2)对?x1,x2∈R+,根据所画下凸函数f(x)=xlnx图象特征指出x1lnx1+x2lnx2≥(x1+x2)[ln(x1+x2)-ln2]与x1lnx1+x2lnx2≥(x1+x2)[ln(x1+x2)-ln2]的大小关系;
(3)当n为正整数时,定义函数N (n)表示n的最大奇因数.如N (3)=3,N (10)=5,….记S(n)=N(1)+N(2)+…+N(2n),若
xi=1,证明:
xilnxi≥-ln2nln
(i,n∈N*).
(1)证明函数f(x)=xlnx是定义域内的下凸函数,并在所给直角坐标系中画出函数f(x)=xlnx的图象;
(2)对?x1,x2∈R+,根据所画下凸函数f(x)=xlnx图象特征指出x1lnx1+x2lnx2≥(x1+x2)[ln(x1+x2)-ln2]与x1lnx1+x2lnx2≥(x1+x2)[ln(x1+x2)-ln2]的大小关系;
(3)当n为正整数时,定义函数N (n)表示n的最大奇因数.如N (3)=3,N (10)=5,….记S(n)=N(1)+N(2)+…+N(2n),若
| 2n |
 |
| i=1 |
| 2n |
 |
| i=1 |
| 1 | ||
|
分析:(1)函数f(x)=xlnx的定义域为(0,+∞),f'(x)=1+lnx,f″(x)=
>0,由此能够证明函数f(x)=xlnx是定义域(0,+∞)内的下凸函数,并作出其图象.
(2)由下凸函数f(x)=xlnx的图象特征可知:
≥f(
),故x1lnx1+x2lnx2≥(x1+x2)[ln(x1+x2)-ln2].
(3)由S(n)=N(1)+N(2)+…+N(2n),知S(n)=4n-1+S(n-1),(n≥1),由此得到证明
xilnxi≥-ln2nln
(i,n∈N*),即证
xilnxi≥-ln2n.可以用数学归纳法进行证明,也可用放缩法进行证明.
| 1 |
| x |
(2)由下凸函数f(x)=xlnx的图象特征可知:
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
(3)由S(n)=N(1)+N(2)+…+N(2n),知S(n)=4n-1+S(n-1),(n≥1),由此得到证明
| 2n |
 |
| i=1 |
| 1 | ||
|
| 2n |
 |
| i=1 |
解答: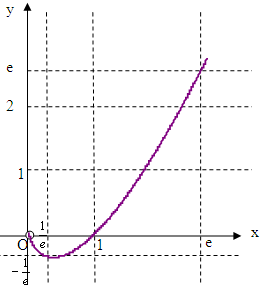 解:(1)函数f(x)=xlnx的定义域为(0,+∞),
解:(1)函数f(x)=xlnx的定义域为(0,+∞),
f'(x)=1+lnx,f″(x)=
>0,
故函数f(x)=xlnx是定义域(0,+∞)内的下凸函数,…(2分)
函数f(x)=xlnx在(0,
]单调递减,在[
,+∞)单调递增,
且f(
)=-
,f(1)=0,f(e)=e,…(3分)
故其图象如下图所示.….(4分)
(2)由下凸函数f(x)=xlnx的图象特征可知:
≥f(
),
故x1lnx1+x2lnx2≥(x1+x2)[ln(x1+x2)-ln2]
≥x1lnx1+x2lnx2≥(x1+x2)[ln(x1+x2)-ln2]
(当且仅当x1=x2时取=号)….(6分)
(3)∵S(n)=N(1)+N(2)+…+N(2n),
∴S(n)=[1+3+5+…+(2n-1)]+[N(2)+N(4)+N(6]+…+N(2n)],
∴S(n)=4n-1+S(n-1),(n≥1),
∵S1=N(1),S(1)=2,…(7分)
∴S(n)=4n-1+4n-2+…+41+2=
…(8分)
∴ln
=-ln2n,
故证明
xilnxi≥-ln2nln
(i,n∈N*)
即证
xilnxi≥-ln2n…(9分)
(证法一)数学归纳法
ⅰ)当n=1时,由(2)知命题成立.
ⅱ)假设当n=k( k∈N*)时命题成立,
即若x1+x2+…+x2k=1,
则x1lnx1+x2lnx2+…+x2klnx2k≥-ln2k…(10分)
当n=k+1时,x1,x2,…,x2k+1-1,x2k+1满足 x1+x2+…+x2k+1-1+x2k+1=1.
设F(x)=x1lnx1+x2lnx2+…+x2k+1-1lnx2k+1-1+x2k+1lnx2k+1,
由(2)得F(x)≥(x1+x2)ln[(x1+x2)-ln2]+…+(x2k+1-1+x2k+1)ln[(x2k+1-1+x2k+1)-ln2]
=(x1+x2)ln(x1+x2)+…+(x2k+1-1+x2k+1)ln(x2k+1-1+x2k+1)-(x1+x2+…+x2k+1)ln2
=(x1+x2)ln(x1+x2)+…+(x2k+1-1+x2k+1)ln(x2k+1-1+x2k+1)-ln2.
由假设可得 F(x)≥-ln2k-ln2=-ln2k+1,命题成立.
所以当 n=k+1时命题成立…(13分)
由ⅰ),ⅱ)可知,对一切正整数n∈N*,命题都成立,
所以 若
xi=1,则
xilnxi≥-ln2n(i,n∈N*).
即有
xilnxi≥-ln2nln
(i,n∈N*). …(14分)
(证法二)若x1+x2+…+x2n=1,
那么由(2)可得x1lnx1+x2lnx2+…+x2nlnx2n≥(x1+x2)ln[(x1+x2)-ln2]+…+(x2n-1+x2n)ln[(x2n-1+x2n)-ln2]…(10分)
=(x1+x2)ln(x1+x2)+…+(x2n-1+x2n)ln(x2n-1+x2n)-(x1+x2+…+x2n)ln2…(11分)
=(x1+x2)ln(x1+x2)+…+(x2n-1+x2n)ln(x2n-1+x2n)-ln2…(12分)
≥(x1+x2+x3+x4)ln(x1+x2+x3+x4)+…(x2n-1+x2n)ln(x2n-1+x2n)-2ln2…(13分)
≥…≥(x1+x2+…+x2n)ln[(x1+x2+…+x2n)-ln2]-(n-1)ln2=-ln2n.
即有
xilnxi≥-ln2nln
(i,n∈N*). …(14分)
 解:(1)函数f(x)=xlnx的定义域为(0,+∞),
解:(1)函数f(x)=xlnx的定义域为(0,+∞),f'(x)=1+lnx,f″(x)=
| 1 |
| x |
故函数f(x)=xlnx是定义域(0,+∞)内的下凸函数,…(2分)
函数f(x)=xlnx在(0,
| 1 |
| e |
| 1 |
| e |
且f(
| 1 |
| e |
| 1 |
| e |
故其图象如下图所示.….(4分)
(2)由下凸函数f(x)=xlnx的图象特征可知:
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
故x1lnx1+x2lnx2≥(x1+x2)[ln(x1+x2)-ln2]
≥x1lnx1+x2lnx2≥(x1+x2)[ln(x1+x2)-ln2]
(当且仅当x1=x2时取=号)….(6分)
(3)∵S(n)=N(1)+N(2)+…+N(2n),
∴S(n)=[1+3+5+…+(2n-1)]+[N(2)+N(4)+N(6]+…+N(2n)],
∴S(n)=4n-1+S(n-1),(n≥1),
∵S1=N(1),S(1)=2,…(7分)
∴S(n)=4n-1+4n-2+…+41+2=
| 4n+2 |
| 3 |
∴ln
| 1 | ||
|
故证明
| 2n |
 |
| i=1 |
| 1 | ||
|
即证
| 2n |
 |
| i=1 |
(证法一)数学归纳法
ⅰ)当n=1时,由(2)知命题成立.
ⅱ)假设当n=k( k∈N*)时命题成立,
即若x1+x2+…+x2k=1,
则x1lnx1+x2lnx2+…+x2klnx2k≥-ln2k…(10分)
当n=k+1时,x1,x2,…,x2k+1-1,x2k+1满足 x1+x2+…+x2k+1-1+x2k+1=1.
设F(x)=x1lnx1+x2lnx2+…+x2k+1-1lnx2k+1-1+x2k+1lnx2k+1,
由(2)得F(x)≥(x1+x2)ln[(x1+x2)-ln2]+…+(x2k+1-1+x2k+1)ln[(x2k+1-1+x2k+1)-ln2]
=(x1+x2)ln(x1+x2)+…+(x2k+1-1+x2k+1)ln(x2k+1-1+x2k+1)-(x1+x2+…+x2k+1)ln2
=(x1+x2)ln(x1+x2)+…+(x2k+1-1+x2k+1)ln(x2k+1-1+x2k+1)-ln2.
由假设可得 F(x)≥-ln2k-ln2=-ln2k+1,命题成立.
所以当 n=k+1时命题成立…(13分)
由ⅰ),ⅱ)可知,对一切正整数n∈N*,命题都成立,
所以 若
| 2n |
 |
| i=1 |
| 2n |
 |
| i=1 |
即有
| 2n |
 |
| i=1 |
| 1 | ||
|
(证法二)若x1+x2+…+x2n=1,
那么由(2)可得x1lnx1+x2lnx2+…+x2nlnx2n≥(x1+x2)ln[(x1+x2)-ln2]+…+(x2n-1+x2n)ln[(x2n-1+x2n)-ln2]…(10分)
=(x1+x2)ln(x1+x2)+…+(x2n-1+x2n)ln(x2n-1+x2n)-(x1+x2+…+x2n)ln2…(11分)
=(x1+x2)ln(x1+x2)+…+(x2n-1+x2n)ln(x2n-1+x2n)-ln2…(12分)
≥(x1+x2+x3+x4)ln(x1+x2+x3+x4)+…(x2n-1+x2n)ln(x2n-1+x2n)-2ln2…(13分)
≥…≥(x1+x2+…+x2n)ln[(x1+x2+…+x2n)-ln2]-(n-1)ln2=-ln2n.
即有
| 2n |
 |
| i=1 |
| 1 | ||
|
点评:本题考查下凸函数的证明,函数图象的画法,不等式的比较和证明,综合性强,难度大,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
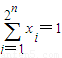 ,证明:
,证明: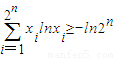
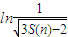 (i,n∈N*).
(i,n∈N*).