题目内容
6.二次函数y=-x2+2$\sqrt{3}$x+1的函数图象与x轴两交点之间的距离为4.分析 令-x2+2$\sqrt{3}$x+1=0的两个根为x1,x2,则二次函数y=-x2+2$\sqrt{3}$x+1的图象与x轴两交点之间的距离为|x1-x2|,进而根据韦达定理的推论2,得到答案.
解答 解:令-x2+2$\sqrt{3}$x+1=0的两个根为x1,x2,
则|x1-x2|=$\frac{\sqrt{△}}{\left|a\right|}$=$\sqrt{12+4}$=4,
∴二次函数y=-x2+2$\sqrt{3}$x+1的图象与x轴两交点之间的距离为4,
故答案为:4
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案
相关题目
16.“x,y,z成等比数列“是“y2=xz”成立的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
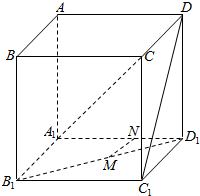 在正方体ABCD-A1B1C1D1中,若M、N分别为B1D1与C1D上的点,且MN⊥B1D,MN⊥C1D1,则MN与A1C的位置关系是MN∥A1C.1.
在正方体ABCD-A1B1C1D1中,若M、N分别为B1D1与C1D上的点,且MN⊥B1D,MN⊥C1D1,则MN与A1C的位置关系是MN∥A1C.1.