题目内容

7．在等差数列{an}中，Sp=q，Sq=q，Sp+q的值为（　　）
A．p+qB．-（p+q）C．p2-q2D．p2+q2

分析 先用p，q表示等差数列{an}中的公差d，再把Sp+q用p，q，d表示，化简可得．

解答 解；设等差数列{an}的首项为a1，公差为d，
则Sp=pa1+$\frac{p（p-1）}{2}$d=q，Sq=qa1+$\frac{q（q-1）}{2}$d=p，
∴d=$\frac{-2（p+q）}{pq}$，设p＜q，
则Sp+q=Sp+ap+1+ap+2+…+ap+q=Sp+Sq+pqd=p+q+pq$\frac{-2（p+q）}{pq}$=-（p+q）
故选：B．

点评 本题考查等差数列的求和公式和通项公式，属基础题．

练习册系列答案
相关题目
17．已知关于x的不等式组$\left\{\begin{array}{l}{（2x-3）（3x+2）≤0}\\{x-a＞0}\end{array}\right.$无实数解，求实数a的取值范围．
18．已知函数f（x）=2x-$\frac{a}{x}$，且f（1）=3．
（1）求a的值；
（2）判断函数的奇偶性并证明．
15．已知函数f（x）=$\left\{\begin{array}{l}{2，x∉[-2，2]}\\{|x|，x∈[-2，2]}\end{array}\right.$，则其最小值为（　　）
A．2B．0C．-2D．不存在
2．求函数f（x）=x2+ax+3在[1，3]上的最大值．
12．设函数f（x）是定义在R上的增函数，如果不等式f（ax2+x-2）＜f（x2-x+1）对于任意x∈[$\frac{3}{2}$，+∞）恒成立，求实数a的取值范围．
3．已知函数f（x）=$\frac{3x+7}{x+2}$，x∈（-2，2）
（1）判断函数的单调性；
（2）解不等式log${\;}_{\frac{1}{2}}$（f（-2m+3））＞log${\;}_{\frac{1}{2}}$（f（m2））．
20．用定义证明：函数f（x）=x+$\frac{2}{x}$在（$\sqrt{2}$，+∞）上是增函数．
1．设函数f（x）=2x，则如图所示的函数图象（　　）
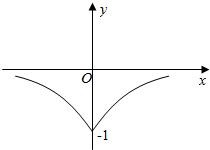
A．y=f（|x|）B．y=-|f（x）|C．y=-f（-|x|）D．y=f（-|x|）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网