题目内容
3.判断函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{-{x}^{2},x<0}\end{array}\right.$的奇偶性.分析 根据函数奇偶性的定义进行判断即可.
解答 解:如x>0,则-x<0,
则f(-x)=-(-x)2=-x2=-f(x),
若x<0,则-x>0,
则f(-x)=(-x)2=x2=-f(x),
当x=0时,f(0)=0,
综上f(-x)=-f(x),
则函数f(x)为奇函数.
点评 本题主要考查函数奇偶性的判断,根据函数奇偶性的定义是解决本题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
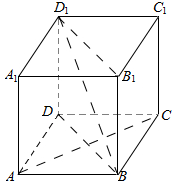 如图,ABCD-A1B1C1D1是棱长为a的正方体.求证:
如图,ABCD-A1B1C1D1是棱长为a的正方体.求证: