题目内容
【题目】如图，在杨辉三角形中，斜线l的上方从1按箭头所示方向可以构成一个“锯齿形”的数列：1，3，3，4，6，5，10，…，记此数列的前n项之和为Sn ， 则S21的值为（ ） 
A.66
B.153
C.295
D.361
【答案】D
【解析】解：从杨辉三角形的生成过程，可以得到你的这个数列的通项公式a（n）． n为偶数时，a（n）=（n+4）/2，
n为奇数时，1=c20=C22 ， 3=C31=C32 ， 6=C42 ， 10=C53=C52 ， …
a（n）=C（n+3）/22=（n+3）（n+1）/8．
然后求前21项和，偶数项和为75，
奇数项和为[（22+42+62+…+222）+2（2+4+6…+22）]/8
=[（22×4×23）+11×24]/8=286，
最后S（21）=361
故选D．
【考点精析】本题主要考查了数列的前n项和的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系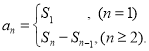
才能正确解答此题．
练习册系列答案
相关题目
【题目】某大学餐饮中心为了了解新生的饮食习惯，利用简单随机抽样的方法在全校一年级学生中进行了抽样调查，调查结果如表所示：
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
（1）根据表中数据，问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”；
（2）根据（1）的结论，你能否提出更好的调查方法来了解该校大学新生的饮食习惯，说明理由．
