题目内容
8.向边长分别为$\sqrt{13}$、5、6的三角形区域内随机投一点D,则该点D与三角形三个顶点距离都大于$\sqrt{3}$的概率为( )| A. | 0 | B. | $1-\frac{π}{3}$ | C. | $1-\frac{π}{6}$ | D. | $1-\frac{π}{8}$ |
分析 根据三角形的面积公式求出三角形的面积,以及点M与三角形三个顶点距离都大于$\sqrt{3}$对应的平面区域,利用几何概型的概率公式进行计算即可.
解答 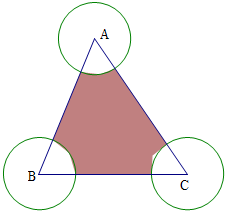 解:设a=5,b=6,c=$\sqrt{13}$,
解:设a=5,b=6,c=$\sqrt{13}$,
则由余弦定理得cosC=$\frac{{5}^{2}+{6}^{2}-13}{2×5×6}$=$\frac{4}{5}$,
则sinC=$\frac{3}{5}$,
则三角形的面积S=$\frac{1}{2}absinC$=9,
则M与三角形三个顶点距离都大于$\sqrt{3}$的面积为9-$\frac{1}{2}×π×3$=9-$\frac{3π}{2}$,
则根据几何概型的概率公式可得所求的概率为$\frac{9-\frac{3}{2}π}{9}$=1-$\frac{π}{6}$,
故选:C.
点评 本题主要考查几何概型的概率的计算,利用余弦定理求出相应的面积是解决本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
19.设复数z1=1+i,z2=x+2i(x∈R),若z1z2为纯虚数,则x=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
16.集合M={x|lgx>0},N={x|x2≤4},则M∩N=( )
| A. | (0,2] | B. | (0,2) | C. | (1,2] | D. | (1,2) |
3.定义在R上的奇函数f(x)和定义在{x|x≠0}上的偶函数g(x)分别满足f(x)=$\left\{\begin{array}{l}{{2}^{x}-1(0≤x<1)}\\{\frac{1}{x}(x≥1)}\end{array}\right.$,g(x)=log2x(x>0),若存在实数a,使得f(a)=g(b)成立,则实数b的取值范围是( )
| A. | [-2,2] | B. | [-$\frac{1}{2}$,0)∪(0,$\frac{1}{2}$] | C. | [-2,-$\frac{1}{2}$]∪[$\frac{1}{2}$,2] | D. | (-∞,-2]∪[2,+∞) |
20.某高中校共有学生1000名,各年级男女学生人数如下表,已知在全校学生中随机抽取1名,抽到高二男生的概率是0.16.
现用分层抽样的方法,在全校抽取40名学生,则应在高三年级抽取的学生人数为15.
| 高一年级 | 高二年级 | 高三年级 | |
| 女生 | 162 | 140 | Y |
| 男生 | 163 | X | 184 |
18.复数$\frac{\sqrt{2}+i}{1-\sqrt{2}i}$=( )
| A. | i | B. | -i | C. | 2($\sqrt{2}$+i) | D. | 1+i |
 底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{{4\sqrt{2}}}{3}$,则该半球的体积为$\frac{4\sqrt{2}π}{3}$.
底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{{4\sqrt{2}}}{3}$,则该半球的体积为$\frac{4\sqrt{2}π}{3}$.