题目内容
18.已知函数f(x)=cos4x+2$\sqrt{3}$sinxcosx-sin4x.(1)求函数f(x)的最小正周期及当x∈[0,$\frac{π}{2}$]时函数f(x)的最小值;
(2)已知a、b、c分别是△ABC的三个内角A、B、C对应的边长,若f(B)=1,b=4,△ABC的面积s=2$\sqrt{3}$,求△ABC的周长.
分析 (1)由三角函数恒等变换化简函数解析式可得f(x)=2sin(2x+$\frac{π}{6}$),由周期公式即可求T,由x∈[0,$\frac{π}{2}$]时,可求2x+$\frac{π}{6}$的范围,从而可求f(x)的范围,即可得解.
(2)由f(B)=2sin(2B+$\frac{π}{6}$)=1,结合角B的范围即可求出B的值,sinB,cosB的值,由s=2$\sqrt{3}$=$\frac{1}{2}$acsinB=$\frac{\sqrt{3}}{4}$ac,可解得ac,由余弦定理可解得a+c=2$\sqrt{10}$,从而可求△ABC的周长.
解答 解:(1)∵f(x)=cos4x+2$\sqrt{3}$sinxcosx-sin4x=$\sqrt{3}$sin2x+cos2x=2sin(2x+$\frac{π}{6}$),
∴函数f(x)的最小正周期T=$\frac{2π}{2}$=π.
∴x∈[0,$\frac{π}{2}$]时,2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
∴sin(2x+$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],f(x)=2sin(2x+$\frac{π}{6}$)∈[-1,2],
∴当x∈[0,$\frac{π}{2}$]时函数f(x)的最小值是:-1.
(2)∵f(B)=2sin(2B+$\frac{π}{6}$)=1,sin(2B+$\frac{π}{6}$)=$\frac{1}{2}$,
又∵0<B<π,可得2B+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{13π}{6}$)
∴可解得:2B+$\frac{π}{6}$=$\frac{5π}{6}$,解得B=$\frac{π}{3}$,sinB=$\frac{\sqrt{3}}{2}$,cosB=$\frac{1}{2}$,
∵s=2$\sqrt{3}$=$\frac{1}{2}$acsinB=$\frac{\sqrt{3}}{4}$ac,可得ac=8,
∴由余弦定理可得:b2=a2+c2-2accosB,可得:16=a2+c2-ac,
∴解得:(a+c)2-3ab=16,即解得:(a+c)2=40,从而有:a+c=2$\sqrt{10}$,
∴△ABC的周长=a+b+c=2$\sqrt{10}$+4.
点评 本题主要考察了余弦定理,三角形面积公式,三角函数恒等变换的应用,考查了同角三角函数基本关系的运用,三角函数的周期性及其求法,综合性较强,属于中档题.

| A. | a≤0 | B. | 0<a<$\frac{1}{2}$ | C. | $\frac{1}{2}$<a<1 | D. | a≤0或a>1 |
 函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2015)的值为( )
函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2015)的值为( )| A. | 0 | B. | 3$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | -$\sqrt{2}$ |
| A. | 0 | B. | $1-\frac{π}{3}$ | C. | $1-\frac{π}{6}$ | D. | $1-\frac{π}{8}$ |
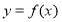 的大致图象如图所示,则函数
的大致图象如图所示,则函数 的解析式应为( )
的解析式应为( )
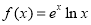 B.
B.
 D.
D.