题目内容
3.定义在R上的奇函数f(x)和定义在{x|x≠0}上的偶函数g(x)分别满足f(x)=$\left\{\begin{array}{l}{{2}^{x}-1(0≤x<1)}\\{\frac{1}{x}(x≥1)}\end{array}\right.$,g(x)=log2x(x>0),若存在实数a,使得f(a)=g(b)成立,则实数b的取值范围是( )| A. | [-2,2] | B. | [-$\frac{1}{2}$,0)∪(0,$\frac{1}{2}$] | C. | [-2,-$\frac{1}{2}$]∪[$\frac{1}{2}$,2] | D. | (-∞,-2]∪[2,+∞) |
分析 根据函数的奇偶性作出函数f(x)和g(x)的图象,利用数形结合即可得到结论.
解答 解:分别作出函数f(x)和g(x)的图象如图,
若若存在实数a,使得f(a)=g(b)成立,
则b一定在函数g(x)使两个函数的函数值重合的区间内,
∵函数f(x)的最大值为1,最小值为-1,
∴由log2x=1,解得x=2,
由log2(-x)=1,解得x=-2,
故b的取值范围是[-2,-$\frac{1}{2}$]∪[$\frac{1}{2}$,2],
故选:C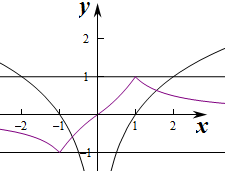
点评 本题主要考查函数奇偶性的应用,利用函数的奇偶性结合数形结合是解决本题的关键.

练习册系列答案
相关题目
14.若集合A={1,m,m2},集合B={2,4},则“m=-2”是“A∩B={4}”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
18.向量$\overrightarrow{a}$与$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{2}$,且$\overrightarrow{a}⊥\overrightarrow{b}$,则|$\overrightarrow{a}+\overrightarrow{b}$|为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{2}$ |
8.向边长分别为$\sqrt{13}$、5、6的三角形区域内随机投一点D,则该点D与三角形三个顶点距离都大于$\sqrt{3}$的概率为( )
| A. | 0 | B. | $1-\frac{π}{3}$ | C. | $1-\frac{π}{6}$ | D. | $1-\frac{π}{8}$ |