题目内容
【题目】已知平面内两点M(4,﹣2),N(2,4).
(1)求MN的垂直平分线方程;
(2)直线l经过点A(3,0),且与直线MN平行,求直线l的方程.
【答案】(1)x﹣3y+1=0;(2)3x+y﹣9=0.
【解析】
(1)由中点坐标公式求得MN的中点坐标,再由两点求斜率公式求得MN所在直线的斜率,进一步得到MN的垂直平分线的斜率,再由直线方程点斜式得答案;
(2)直接由直线方程点斜式可得过点A(3,0),且与直线MN平行的直线l的方程.
解:(1)∵M(4,﹣2),N(2,4),
∴M,N的中点坐标为(3,1),又![]() ,
,
∴MN的垂直平分线的斜率为![]() ,则MN的垂直平分线方程为y﹣1
,则MN的垂直平分线方程为y﹣1![]() (x﹣2),
(x﹣2),
即x﹣3y+1=0;
(2)∵直线l与直线MN平行,∴直线l的斜率为﹣3,
又直线l经过点A(3,0),∴直线l的方程为y=﹣3(x﹣3),
即3x+y﹣9=0.

 阅读快车系列答案
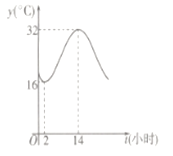
阅读快车系列答案【题目】某种新产品投放市场一段时间后,经过调研获得了时间![]() (天数)与销售单价
(天数)与销售单价![]() (元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
(元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
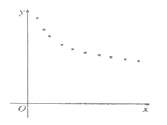
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作价格
哪一个更适宜作价格![]() 关于时间
关于时间![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若该产品的日销售量![]() (件)与时间
(件)与时间![]() 的函数关系为
的函数关系为![]() (
(![]() ),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为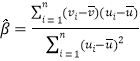 ,
,![]() .
.
【题目】随着新高考改革的不断深入,高中学生生涯规划越来越受到社会的关注.一些高中已经开始尝试开设学生生涯规划选修课程,并取得了一定的成果.下表为某高中为了调查学生成绩与选修生涯规划课程的关系,随机抽取50名学生的统计数据.
成绩优秀 | 成绩不够优秀 | 总计 | |
选修生涯规划课 | 15 | 10 | 25 |
不选修生涯规划课 | 6 | 19 | 25 |
总计 | 21 | 29 | 50 |
(Ⅰ)根据列联表运用独立性检验的思想方法能否有![]() 的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
(Ⅱ)如果从全校选修生涯规划课的学生中随机地抽取3名学生,求抽到成绩不够优秀的学生人数![]() 的分布列和数学期望(将频率当作概率计算).
的分布列和数学期望(将频率当作概率计算).
参考附表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式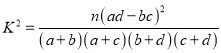 ,其中
,其中![]() .
.
【题目】为响应德智体美劳的教育方针,唐徕回中高一年级举行了由全体学生参加的一分钟跳绳比赛,计分规则如下:
每分钟跳绳个数 |
|
|
|
| 185以上 |
得分 | 16 | 17 | 18 | 19 | 20 |
年级组为了了解学生的体质,随机抽取了100名学生,统计了他的跳绳个数,并绘制了如下样本频率直方图:
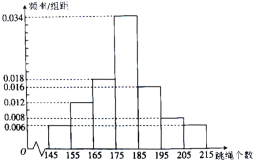
(1)现从这100名学生中,任意抽取2人,求两人得分之和小于35分的概率(结果用最简分数表示);
(2)若该校高二年级2000名学生,所有学生的一分钟跳绳个数![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() ,
,![]() 为样本平均数的估计值(同一组中数据以这组数据所在区间的中点值为代表).利用所得到的正态分布模型解决以下问题:
为样本平均数的估计值(同一组中数据以这组数据所在区间的中点值为代表).利用所得到的正态分布模型解决以下问题:
①估计每分钟跳绳164个以上的人数(四舍五入到整数)
②若在全年级所有学生中随机抽取3人,记每分钟跳绳在179个以上的人数为![]() ,求
,求![]() 的分布列和数学期望与方差.
的分布列和数学期望与方差.
(若随机变量![]() 服从正态分布
服从正态分布![]() 则
则![]() ,
,![]() ,
,