题目内容
【题目】定义在![]() 上的函数
上的函数![]() 满足下列两个条件:(1)对任意的
满足下列两个条件:(1)对任意的![]() 恒有
恒有![]() 成立;(2)当
成立;(2)当![]() 时,
时,![]() ;记函数
;记函数![]() ,若函数
,若函数![]() 恰有两个零点,则实数
恰有两个零点,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根据题中的条件得到函数的解析式为:f(x)=﹣x+2b,x∈(b,2b],又因为f(x)=k(x﹣1)的函数图象是过定点(1,0)的直线,再结合函数的图象根据题意求出参数的范围即可
因为对任意的x∈(1,+∞)恒有f(2x)=2f(x)成立,
且当x∈(1,2]时,f(x)=2﹣x;
f(x)=2(2![]() )=4﹣x,x∈(2,4],
)=4﹣x,x∈(2,4],
f(x)=4(2![]() )=8﹣x,x∈(4,8],
)=8﹣x,x∈(4,8],
…
所以f(x)=﹣x+2b,x∈(b,2b].(b取1,2,4…)
由题意得f(x)=k(x﹣1)的函数图象是过定点(1,0)的直线,
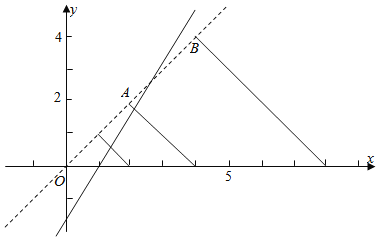
如图所示只需过(1,0)的直线与线段AB相交即可(可以与B点重合但不能与A点重合)kPA![]() 2,kPB
2,kPB![]() ,
,
所以可得k的范围为![]()
故选:C.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目


