题目内容
【题目】已知函数f(x)=loga![]() (a>0且a≠1).
(a>0且a≠1).
(1)求f(x)的定义域;
(2)当0<a<1时,判断f(x)在(2,+∞)的单惆性;
(3)是否存在实数a,使得当f(x)的定义域为[m,n]时,值域为[1+logan,1+1ogam],若存在,求出实数a的范围;若不存在,请说明理由.
【答案】(1)![]() ; (2)见解析;(3)存在这样的实数a∈(0,
; (2)见解析;(3)存在这样的实数a∈(0,![]() )符合题意.
)符合题意.
【解析】
(1)由对数式的真数大于0求解函数的定义域;
(2)利用分离常数法判断真数![]() 的单调性,再由复合函数的单调性得答案;
的单调性,再由复合函数的单调性得答案;
(3)把![]() 的定义域为
的定义域为![]() ,
,![]() 时值域为
时值域为![]() ,
,![]() 转化为
转化为![]() 在
在![]() 上为减函数,进一步得到
上为减函数,进一步得到![]() 在
在![]() 上有两个互异实根,令
上有两个互异实根,令![]() ,转化为关于
,转化为关于![]() 的不等式组求解.
的不等式组求解.
(1)由![]() >0,得x<-2或x>2.
>0,得x<-2或x>2.
∴f(x)的定义域为(-∞,-2)∪(2,+∞);
(2)令t(x)=![]() =1-
=1-![]() ,t(x)在(2,+∞)上为增函数,
,t(x)在(2,+∞)上为增函数,
又0<a<1,
∴f(x)在(2,+∞)上为减函数;
(3)假设存在这样的实数a,使得当f(x)的定义域为[m,n]时,值域为[1+logan,1+1ogam],
由m<n且1+logan,1+1ogam,
即m<n1+logan,1+1ogam,可得0<a<1.
t(x)=1-![]() 在(2,+∞)上为增函数,
在(2,+∞)上为增函数,
又∵0<a<1,
∴f(x)在(2,+∞)上为减函数,
∴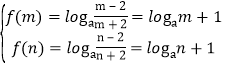 ,
,
∴![]() ,即
,即![]() 在(2,+∞)上有两个互异实根,
在(2,+∞)上有两个互异实根,
令g(x)=ax2+(2a-1)x+2,
则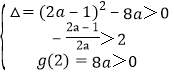 ,解得0<a<
,解得0<a<![]() .
.
又∵0<a<1,故存在这样的实数a∈(0,![]() )符合题意.
)符合题意.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目


